1988 AIME Problems/Problem 10
Contents
Problem
A convex polyhedron has for its faces 12 squares, 8 regular hexagons, and 6 regular octagons. At each vertex of the polyhedron one square, one hexagon, and one octagon meet. How many segments joining vertices of the polyhedron lie in the interior of the polyhedron rather than along an edge or a face?
Solution 1
The number of segments joining the vertices of the polyhedron is  . We must now subtract out those segments that lie along an edge or a face.
. We must now subtract out those segments that lie along an edge or a face.
Since every vertex of the polyhedron lies on exactly one vertex of a square/hexagon/octagon, we have that ![]() .
.
Each vertex is formed by the intersection of 3 edges. Since every edge is counted twice, once at each of its endpoints, the number of edges ![]() is
is ![]() .
.
Each of the segments lying on a face of the polyhedron must be a diagonal of that face. Each square contributes ![]() diagonals, each hexagon
diagonals, each hexagon ![]() , and each octagon
, and each octagon ![]() . The number of diagonals is thus
. The number of diagonals is thus ![]() .
.
Subtracting, we get that the number of space diagonals is ![]() .
.
Solution 2
We first find the number of vertices on the polyhedron:
There are 4 corners per square, 6 corners per hexagon, and 8 corners per octagon. Each vertex is where 3 corners coincide, so we count the corners and divide by 3. ![]() .
.
We know that all vertices look the same (from the problem statement), so we should find the number of line segments originating from a vertex, and multiply that by the number of vertices, and divide by 2 (because each space diagonal is counted twice because it has two endpoints).
Counting the vertices that are on the same face as an arbitrary vertex, we find that there are 13 vertices that aren't possible endpoints of a line originating from the vertex in the middle of the diagram.
You can draw a diagram to count this better: 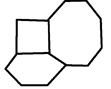 Since 13 aren't possible endpoints, that means that there are 35 possible endpoints per vertex.
The total number of segments joining vertices that aren't on the same face is
Since 13 aren't possible endpoints, that means that there are 35 possible endpoints per vertex.
The total number of segments joining vertices that aren't on the same face is ![]()
See also
| 1988 AIME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 9 |
Followed by Problem 11 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. 









