Difference between revisions of "1988 AIME Problems/Problem 12"
m (img) |
I like pie (talk | contribs) (→Solution) |
||
| Line 21: | Line 21: | ||
<cmath>3[(a + 3)(b + 3) + (b + 3)(c + 3) + (c + 3)(a + 3)] = (a+3)(b+3)(c+3)</cmath> | <cmath>3[(a + 3)(b + 3) + (b + 3)(c + 3) + (c + 3)(a + 3)] = (a+3)(b+3)(c+3)</cmath> | ||
<cmath>3(ab + bc + ca) + 18(a + b + c) + 81 = abc + 3(ab + bc + ca) + 9(a + b + c) + 27</cmath> | <cmath>3(ab + bc + ca) + 18(a + b + c) + 81 = abc + 3(ab + bc + ca) + 9(a + b + c) + 27</cmath> | ||
| − | <cmath>9(a + b + c) + 54 = | + | <cmath>9(a + b + c) + 54 = abc=\boxed{441}</cmath> |
| − | |||
== See also == | == See also == | ||
Revision as of 19:17, 10 April 2008
Problem
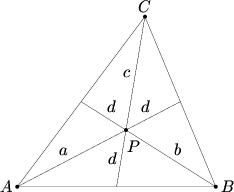
Let ![]() be an interior point of triangle
be an interior point of triangle ![]() and extend lines from the vertices through
and extend lines from the vertices through ![]() to the opposite sides. Let
to the opposite sides. Let ![]() ,
, ![]() ,
, ![]() , and
, and ![]() denote the lengths of the segments indicated in the figure. Find the product
denote the lengths of the segments indicated in the figure. Find the product ![]() if
if ![]() and
and ![]() .
.
Solution
Call the cevians AD, BE, and CF. Using area ratios (![]() and
and ![]() have the same base), we have:
have the same base), we have:
![]()
Similarily, ![]() and
and ![]() .
.
Then,
![]()
The identity ![]() is a form of Ceva's Theorem.
is a form of Ceva's Theorem.
Plugging in ![]() , we get
, we get
![]()
![]()
![]()
![]()
See also
| 1988 AIME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 11 |
Followed by Problem 13 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||