Difference between revisions of "1988 AIME Problems/Problem 7"
Mathgeek2006 (talk | contribs) m (→Solution) |
Burunduchok (talk | contribs) m (→Solution) |
||
| Line 18: | Line 18: | ||
</cmath> | </cmath> | ||
| − | The postive value of <math>h = 11</math>, so the area is <math>\frac{1}{2}(17 + 3)\cdot 11 = 110</math>. | + | The postive value of <math>h = 11</math>, so the area is <math>\frac{1}{2}(17 + 3)\cdot 11 = \boxed{110}</math>. |
== See also == | == See also == | ||
Revision as of 18:40, 23 April 2017
Problem
In triangle ![]() ,
, ![]() , and the altitude from
, and the altitude from ![]() divides
divides ![]() into segments of length 3 and 17. What is the area of triangle
into segments of length 3 and 17. What is the area of triangle ![]() ?
?
Solution
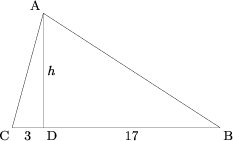
Let ![]() be the intersection of the altitude with
be the intersection of the altitude with ![]() , and
, and ![]() be the length of the altitude. Without loss of generality, let
be the length of the altitude. Without loss of generality, let ![]() and
and ![]() . Then
. Then ![]() and
and ![]() . Using the tangent sum formula,
. Using the tangent sum formula,

The postive value of ![]() , so the area is
, so the area is ![]() .
.
See also
| 1988 AIME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 6 |
Followed by Problem 8 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. 









