1989 AIME Problems
| 1989 AIME (Answer Key) | AoPS Contest Collections • PDF | ||
|
Instructions
| ||
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
Contents
Problem 1
Compute ![]() .
.
Problem 2
Ten points are marked on a circle. How many distinct convex polygons of three or more sides can be drawn using some (or all) of the ten points as vertices?
Problem 3
Suppose ![]() is a positive integer and
is a positive integer and ![]() is a single digit in base 10. Find
is a single digit in base 10. Find ![]() if
if
Problem 4
If ![]() are consecutive positive integers such that
are consecutive positive integers such that ![]() is a perfect square and
is a perfect square and ![]() is a perfect cube, what is the smallest possible value of
is a perfect cube, what is the smallest possible value of ![]() ?
?
Problem 5
When a certain biased coin is flipped five times, the probability of getting heads exactly once is not equal to ![]() and is the same as that of getting heads exactly twice. Let
and is the same as that of getting heads exactly twice. Let ![]() , in lowest terms, be the probability that the coin comes up heads in exactly
, in lowest terms, be the probability that the coin comes up heads in exactly ![]() out of
out of ![]() flips. Find
flips. Find ![]() .
.
Problem 6
Two skaters, Allie and Billie, are at points ![]() and
and ![]() , respectively, on a flat, frozen lake. The distance between
, respectively, on a flat, frozen lake. The distance between ![]() and
and ![]() is
is ![]() meters. Allie leaves
meters. Allie leaves ![]() and skates at a speed of
and skates at a speed of ![]() meters per second on a straight line that makes a
meters per second on a straight line that makes a ![]() angle with
angle with ![]() . At the same time Allie leaves
. At the same time Allie leaves ![]() , Billie leaves
, Billie leaves ![]() at a speed of
at a speed of ![]() meters per second and follows the straight path that produces the earliest possible meeting of the two skaters, given their speeds. How many meters does Allie skate before meeting Billie?
meters per second and follows the straight path that produces the earliest possible meeting of the two skaters, given their speeds. How many meters does Allie skate before meeting Billie?
![[asy] pointpen=black; pathpen=black+linewidth(0.7); pair A=(0,0),B=(10,0),C=6*expi(pi/3); D(B--A); D(A--C,EndArrow); MP("A",A,SW);MP("B",B,SE);MP("60^{\circ}",A+(0.3,0),NE);MP("100",(A+B)/2); [/asy]](http://latex.artofproblemsolving.com/a/3/0/a30f95a4bc471ad519d35b683f2f319118167660.png)
Problem 7
If the integer ![]() is added to each of the numbers
is added to each of the numbers ![]() ,
, ![]() , and
, and ![]() , one obtains the squares of three consecutive terms of an arithmetic series. Find
, one obtains the squares of three consecutive terms of an arithmetic series. Find ![]() .
.
Problem 8
Assume that ![]() are real numbers such that
are real numbers such that
 Find the value of
Find the value of ![]() .
.
Problem 9
One of Euler's conjectures was disproved in the 1960s by three American mathematicians when they showed there was a positive integer such that ![]() Find the value of
Find the value of ![]() .
.
Problem 10
Let ![]() ,
, ![]() ,
, ![]() be the three sides of a triangle, and let
be the three sides of a triangle, and let ![]() ,
, ![]() ,
, ![]() , be the angles opposite them. If
, be the angles opposite them. If ![]() , find
, find
Problem 11
A sample of 121 integers is given, each between 1 and 1000 inclusive, with repetitions allowed. The sample has a unique mode (most frequent value). Let ![]() be the difference between the mode and the arithmetic mean of the sample. What is the largest possible value of
be the difference between the mode and the arithmetic mean of the sample. What is the largest possible value of ![]() ? (For real
? (For real ![]() ,
, ![]() is the greatest integer less than or equal to
is the greatest integer less than or equal to ![]() .)
.)
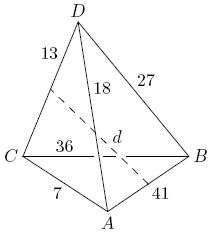
Problem 12
Let ![]() be a tetrahedron with
be a tetrahedron with ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , as shown in the figure. Let
, as shown in the figure. Let ![]() be the distance between the midpoints of edges
be the distance between the midpoints of edges ![]() and
and ![]() . Find
. Find ![]() .
.
Problem 13
Let ![]() be a subset of
be a subset of ![]() such that no two members of
such that no two members of ![]() differ by
differ by ![]() or
or ![]() . What is the largest number of elements
. What is the largest number of elements ![]() can have?
can have?
Problem 14
Given a positive integer ![]() , it can be shown that every complex number of the form
, it can be shown that every complex number of the form ![]() , where
, where ![]() and
and ![]() are integers, can be uniquely expressed in the base
are integers, can be uniquely expressed in the base ![]() using the integers
using the integers ![]() as digits. That is, the equation
as digits. That is, the equation
is true for a unique choice of non-negative integer ![]() and digits
and digits ![]() chosen from the set
chosen from the set ![]() , with
, with ![]() . We write
. We write
to denote the base ![]() expansion of
expansion of ![]() . There are only finitely many integers
. There are only finitely many integers ![]() that have four-digit expansions
that have four-digit expansions
Find the sum of all such ![]() .
.
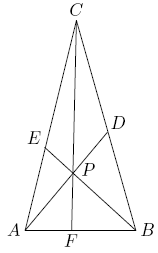
Problem 15
Point ![]() is inside
is inside ![]() . Line segments
. Line segments ![]() ,
, ![]() , and
, and ![]() are drawn with
are drawn with ![]() on
on ![]() ,
, ![]() on
on ![]() , and
, and ![]() on
on ![]() (see the figure below). Given that
(see the figure below). Given that ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , find the area of
, find the area of ![]() .
.
See also
| 1989 AIME (Problems • Answer Key • Resources) | ||
| Preceded by 1988 AIME Problems |
Followed by 1990 AIME Problems | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
- American Invitational Mathematics Examination
- AIME Problems and Solutions
- Mathematics competition resources
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.