Difference between revisions of "1995 AIME Problems/Problem 9"
Dgreenb801 (talk | contribs) (→Solution) |
Dgreenb801 (talk | contribs) (→Solution) |
||
| Line 6: | Line 6: | ||
== Solution == | == Solution == | ||
| − | Let <math>\angle CAM=x</math>, <math>\ | + | Let <math>\angle CAM=x</math>, <math>\angle CDM=3x</math>. Then, <math>(tan 3x)/(tan x)=(CM/1)/(CM/11)=11</math>. Expanding tan 3x using the angle sum formula gives <math>tan 3x=(3tan x-tan^3x)/(1-3tan^2x)</math>. Thus, <math>(3-tan^2x)/(1-3tan^2x)=11</math>. Solving, we get <math>tan x=1/2</math>. Hence, <math>CM=11/2</math> and AC=<math>11\sqrt{5}/2</math> by Pythag. The total perimeter is double the sum of these, which is <math>\sqrt{605}+11</math>. The answer is then <math>616</math>. |
== See also == | == See also == | ||
Revision as of 20:15, 17 June 2008
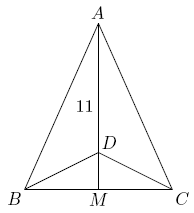
Problem
Triangle ![]() is isosceles, with
is isosceles, with ![]() and altitude
and altitude ![]() Suppose that there is a point
Suppose that there is a point ![]() on
on ![]() with
with ![]() and
and ![]() Then the perimeter of
Then the perimeter of ![]() may be written in the form
may be written in the form ![]() where
where ![]() and
and ![]() are integers. Find
are integers. Find ![]()
Solution
Let ![]() ,
, ![]() . Then,
. Then, ![]() . Expanding tan 3x using the angle sum formula gives
. Expanding tan 3x using the angle sum formula gives ![]() . Thus,
. Thus, ![]() . Solving, we get
. Solving, we get ![]() . Hence,
. Hence, ![]() and AC=
and AC=![]() by Pythag. The total perimeter is double the sum of these, which is
by Pythag. The total perimeter is double the sum of these, which is ![]() . The answer is then
. The answer is then ![]() .
.