Difference between revisions of "1995 AIME Problems/Problem 9"
Dgreenb801 (talk | contribs) (→Solution) |
(tex fixes) |
||
| Line 1: | Line 1: | ||
== Problem == | == Problem == | ||
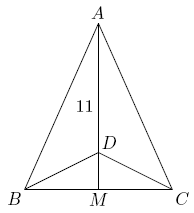
| − | Triangle <math> | + | Triangle <math>ABC</math> is [[isosceles triangle|isosceles]], with <math>AB=AC</math> and [[altitude]] <math>AM=11.</math> Suppose that there is a point <math>D</math> on <math>\overline{AM}</math> with <math>AD=10</math> and <math>\angle BDC=3\angle BAC.</math> Then the perimeter of <math>\triangle ABC</math> may be written in the form <math>a+\sqrt{b},</math> where <math>a</math> and <math>b</math> are integers. Find <math>a+b.</math> |
| − | [[Image:AIME_1995_Problem_9.png]] | + | [[Image:AIME_1995_Problem_9.png|center]] |
== Solution == | == Solution == | ||
| + | Let <math>x=\angle CAM</math>, so <math>3x=\angle CDM</math>. Then, <math>\frac{\tan 3x}{\tan x}=\frac{CM/1}{CM/11}=11</math>. Expanding <math>\tan 3x</math> using the angle sum identity gives <cmath>\tan 3x=\tan(2x+x)=\frac{3\tan x-\tan^3x}{1-3\tan^2x}.</cmath> Thus, <math>\frac{3-\tan^2x}{1-3\tan^2x}=11</math>. Solving, we get <math>\tan x= \frac 12</math>. Hence, <math>CM=\frac{11}2</math> and <math>AC= \frac{11\sqrt{5}}2</math> by the [[Pythagorean Theorem]]. The total perimeter is <math>2(AC + CM) = \sqrt{605}+11</math>. The answer is thus <math>a+b=\boxed{616}</math>. | ||
| − | + | == See also == | |
| + | {{AIME box|year=1995|num-b=8|num-a=10}} | ||
| − | + | [[Category:Intermediate Geometry Problems]] | |
| − | + | [[Category:Intermediate Trigonometry Problems]] | |
| − | |||
| − | |||
Revision as of 12:42, 18 June 2008
Problem
Triangle ![]() is isosceles, with
is isosceles, with ![]() and altitude
and altitude ![]() Suppose that there is a point
Suppose that there is a point ![]() on
on ![]() with
with ![]() and
and ![]() Then the perimeter of
Then the perimeter of ![]() may be written in the form
may be written in the form ![]() where
where ![]() and
and ![]() are integers. Find
are integers. Find ![]()
Solution
Let ![]() , so
, so ![]() . Then,
. Then, ![]() . Expanding
. Expanding ![]() using the angle sum identity gives
using the angle sum identity gives ![]() Thus,
Thus, ![]() . Solving, we get
. Solving, we get ![]() . Hence,
. Hence, ![]() and
and ![]() by the Pythagorean Theorem. The total perimeter is
by the Pythagorean Theorem. The total perimeter is ![]() . The answer is thus
. The answer is thus ![]() .
.
See also
| 1995 AIME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 8 |
Followed by Problem 10 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||