Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "1998 AIME Problems/Problem 10"

(fmt, failed to parse!!)
(→‎Solution: cleanup)
Line 15: Line 15:
 
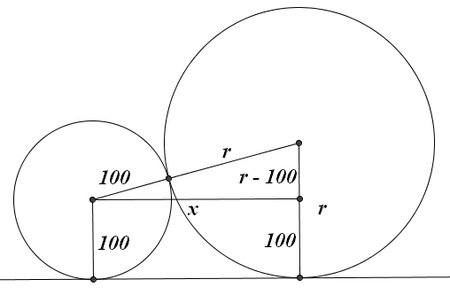
If we draw the segment containing the centers and the radii [[perpendicular]] to the flat surface, we get a [[trapezoid]]; if we draw the segment parallel to the surface that connects the center of the smaller sphere to the radii of the larger, we get a right triangle. Call that segment <math>x</math>. Then by the [[Pythagorean Theorem]]:
 
If we draw the segment containing the centers and the radii [[perpendicular]] to the flat surface, we get a [[trapezoid]]; if we draw the segment parallel to the surface that connects the center of the smaller sphere to the radii of the larger, we get a right triangle. Call that segment <math>x</math>. Then by the [[Pythagorean Theorem]]:
  
−
:<math>x^2 + (r-100)^2 = (r+100)^2</math>
+
<cmath>x^2 + (r-100)^2 = (r+100)^2 \Longrightarrow x = 20\sqrt{r}</cmath>
−
:<math>x^2 = 400r</math>
 
−
:<math>x = 20\sqrt{r}</math>
 
−
 
 
−
Now let us examine the top view again:
 
  
 
[[Image:1998_AIME-10c.png|450px]]
 
[[Image:1998_AIME-10c.png|450px]]
  
−
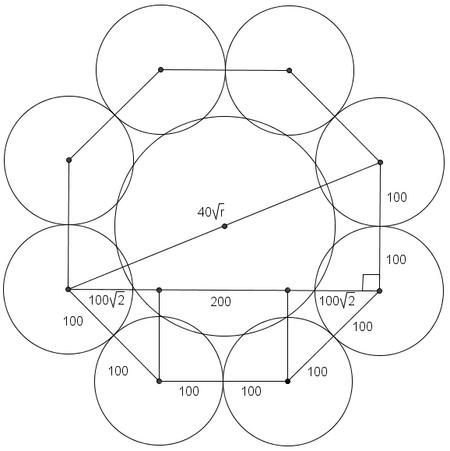
<math>x</math> is the distance from one of the vertices of the octagon to the center, so the diagonal of the octagon is of length <math>\displaystyle 2x = \displaystyle 40\sqrt{r} \displaystyle</math>. We can draw another [[right triangle]] as shown above. One leg has a length of <math>200</math>. The other can be found by partitioning the leg into three sections and using <math>45-45-90 \triangle</math>s to see that the leg is <math>100\sqrt{2} + 200 + 100\sqrt{2} = 200(\sqrt{2} + 1)</math>. Pythagorean Theorem:
+
<math>x</math> is the distance from one of the vertices of the octagon to the center, so the diagonal of the octagon is of length <math>2x =40\sqrt{r}</math>. We can draw another [[right triangle]] as shown above. One leg has a length of <math>200</math>. The other can be found by partitioning the leg into three sections and using <math>45-45-90 \triangle</math>s to see that the leg is <math>100\sqrt{2} + 200 + 100\sqrt{2} = 200(\sqrt{2} + 1)</math>. Pythagorean Theorem:
  
−
<div style="text-align:center;"><math>200^2 + [200(\sqrt{2}+1)]^2 = (40\sqrt{r})^2</math><br />
+
<cmath>\begin{eqnarray*}
−
<math>200^2[(1 + \sqrt{2})^2 + 1] = 1600r</math><br />
+
(40\sqrt{r})^2 &=& 200^2 + [200(\sqrt{2}+1)]^2\\
−
<math>\displaystyle 25(4 + 2\sqrt{2}) = r</math><br />
+
1600r &=& 200^2[(1 + \sqrt{2})^2 + 1] \\
−
<math>r = 100 + 50\sqrt{2}</math></div>
+
r &=& 100 + 50\sqrt{2}</cmath>
  
−
Thus <math>a + b + c = 100 + 50 + 2 = 152</math>.
+
Thus <math>a + b + c = 100 + 50 + 2 = \boxed{152}</math>.
  
 
== See also ==
 
== See also ==

Revision as of 19:40, 6 January 2008

Problem

Eight spheres of radius 100 are placed on a flat surface so that each sphere is tangent to two others and their centers are the vertices of a regular octagon. A ninth sphere is placed on the flat surface so that it is tangent to each of the other eight spheres. The radius of this last sphere is $\displaystyle a + \displaystyle b\sqrt {c} \displaystyle,$ where $a, b,$ and $c$ are positive integers, and $c$ is not divisible by the square of any prime. Find $\displaystyle a + b + c$.

Solution

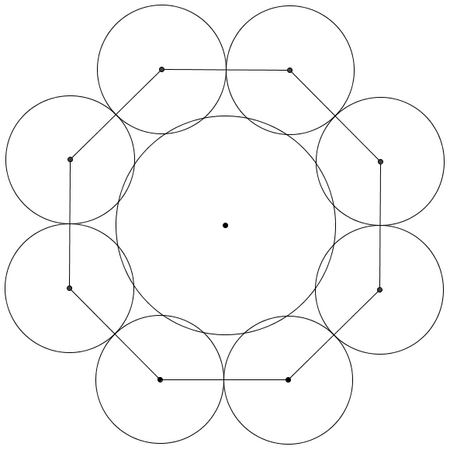
The key is to realize the significance that the figures are spheres, not circles. The 2D analogue of the diagram onto the flat surface will not contain 8 circles tangent to a ninth one; instead the circles will overlap since the middle sphere has a larger radius and will sort of “bulge” out.

1998 AIME-10a.png

Let us examine the relation between one of the outside 8 spheres and the center one (with radius $r$):

1998 AIME-10b.png

If we draw the segment containing the centers and the radii perpendicular to the flat surface, we get a trapezoid; if we draw the segment parallel to the surface that connects the center of the smaller sphere to the radii of the larger, we get a right triangle. Call that segment $x$. Then by the Pythagorean Theorem:

\[x^2 + (r-100)^2 = (r+100)^2 \Longrightarrow x = 20\sqrt{r}\]

1998 AIME-10c.png

$x$ is the distance from one of the vertices of the octagon to the center, so the diagonal of the octagon is of length $2x =40\sqrt{r}$. We can draw another right triangle as shown above. One leg has a length of $200$. The other can be found by partitioning the leg into three sections and using $45-45-90 \triangle$s to see that the leg is $100\sqrt{2} + 200 + 100\sqrt{2} = 200(\sqrt{2} + 1)$. Pythagorean Theorem: 

\begin{eqnarray*}
(40\sqrt{r})^2 &=& 200^2 + [200(\sqrt{2}+1)]^2\\
1600r &=& 200^2[(1 + \sqrt{2})^2 + 1] \\
r &=& 100 + 50\sqrt{2} (Error compiling LaTeX. Unknown error_msg)

Thus $a + b + c = 100 + 50 + 2 = \boxed{152}$.

See also

1998 AIME (Problems • Answer Key • Resources)
Preceded by
Problem 9 		Followed by
Problem 11
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions
Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=1998_AIME_Problems/Problem_10&oldid=22035"