Difference between revisions of "2001 AIME I Problems/Problem 6"
Mathcool2009 (talk | contribs) (→Solution 2) |
(→Solution 1) |
||
| Line 11: | Line 11: | ||
The red path corresponds to the sequence of rolls <math>2, 3, 5, 5</math>. This establishes a one-to-one correspondence between valid dice roll sequences and block walking paths. | The red path corresponds to the sequence of rolls <math>2, 3, 5, 5</math>. This establishes a one-to-one correspondence between valid dice roll sequences and block walking paths. | ||
| − | The solution to this problem is therefore <math>\dfrac{\binom{9}{4}}{6^4} = | + | The solution to this problem is therefore <math>\dfrac{\binom{9}{4}}{6^4} = {\dfrac{7}{72}}=\boxed{79}</math>. |
=== Solution 2 === | === Solution 2 === | ||
Revision as of 13:38, 12 February 2018
Problem
A fair die is rolled four times. The probability that each of the final three rolls is at least as large as the roll preceding it may be expressed in the form ![]() where
where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]() .
.
Contents
Solutions
Solution 1
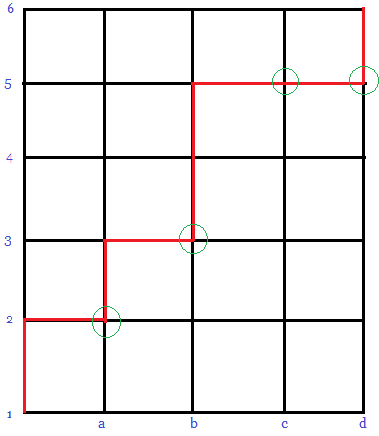
Recast the problem entirely as a block-walking problem. Call the respective dice ![]() . In the diagram below, the lowest
. In the diagram below, the lowest ![]() -coordinate at each of
-coordinate at each of ![]() ,
, ![]() ,
, ![]() , and
, and ![]() corresponds to the value of the roll.
corresponds to the value of the roll.
The red path corresponds to the sequence of rolls ![]() . This establishes a one-to-one correspondence between valid dice roll sequences and block walking paths.
. This establishes a one-to-one correspondence between valid dice roll sequences and block walking paths.
The solution to this problem is therefore ![]() .
.
Solution 2
If we take any combination of four numbers, there is only one way to order them in a non-decreasing order. It suffices now to find the number of combinations for four numbers from ![]() . We can visualize this as taking the four dice and splitting them into 6 slots (each slot representing one of {1,2,3,4,5,6}), or dividing them amongst 5 separators. Thus, there are
. We can visualize this as taking the four dice and splitting them into 6 slots (each slot representing one of {1,2,3,4,5,6}), or dividing them amongst 5 separators. Thus, there are  outcomes of four dice. The solution is therefore
outcomes of four dice. The solution is therefore ![]() , and
, and ![]() .
.
Solution 3
Call the dice rolls ![]() . The difference between the
. The difference between the ![]() and
and ![]() distinguishes the number of possible rolls there are.
distinguishes the number of possible rolls there are.
- If
 , then the values of
, then the values of  are set, and so there are
are set, and so there are  values for
values for  .
. - If
 , then there are
, then there are  ways to arrange for values of
ways to arrange for values of  , but only
, but only  values for
values for  .
. - If
 , then there are
, then there are  ways to arrange
ways to arrange  , and there are only
, and there are only  values for
values for  .
.
Continuing, we see that the sum is equal to  . The requested probability is
. The requested probability is ![]() .
.
Solution 4
The dice rolls can be in the form
ABCD
AABC
AABB
AAAB
AAAA
where A, B, C, D are some possible value of the dice rolls. (These forms are not keeping track of whether or not the dice are in ascending order, just the possible outcomes.)
- Now, for the first case, there are
 ways for this. We do not have to consider the order because the combination counts only one of the permutations; we can say that it counts the correct (ascending order) permutation.
ways for this. We do not have to consider the order because the combination counts only one of the permutations; we can say that it counts the correct (ascending order) permutation. - Second case:
 ways to pick 3 numbers,
ways to pick 3 numbers,  ways to pick 1 of those 3 to duplicate. A total of 60 for this case.
ways to pick 1 of those 3 to duplicate. A total of 60 for this case. - Third case:
 ways to pick 2 numbers. We will duplicate both, so nothing else in this case matters.
ways to pick 2 numbers. We will duplicate both, so nothing else in this case matters. - Fourth case:
 ways to pick 2 numbers. We pick one to duplicate with
ways to pick 2 numbers. We pick one to duplicate with  , so there are a total of 30 in this case.
, so there are a total of 30 in this case. - Fifth case:
 ; all get duplicated so nothing else matters.
; all get duplicated so nothing else matters.
There are a total of ![]() possible dice rolls.
possible dice rolls.
Thus,
Solution 5
Consider the number of possible dice roll combinations which work after ![]() roll, after
roll, after ![]() rolls, and so on. There is 6 possible rolls for the first dice. If the number rolled is a 1, then there are 6 further values that are possible for the second dice; if the number rolled is a 2, then there are 5 further values that are possible for the second dice, and so on.
rolls, and so on. There is 6 possible rolls for the first dice. If the number rolled is a 1, then there are 6 further values that are possible for the second dice; if the number rolled is a 2, then there are 5 further values that are possible for the second dice, and so on.
Suppose we generalize this as a function, say ![]() return the number of possible combinations after
return the number of possible combinations after ![]() rolls and
rolls and ![]() being the beginning value of the first roll. It becomes clear that from above,
being the beginning value of the first roll. It becomes clear that from above, ![]() ; every value of
; every value of ![]() after that is equal to the sum of the number of combinations of
after that is equal to the sum of the number of combinations of ![]() rolls that have a starting value of at least
rolls that have a starting value of at least ![]() . If we slowly count through and add up all the possible combinations we get
. If we slowly count through and add up all the possible combinations we get ![]() possibilities.
possibilities.
Solution 6
In a manner similar to the above solution, instead consider breaking it down into two sets of two dice rolls. The first subset must have a maximum value which is ![]() the minimum value of the second subset.
the minimum value of the second subset.
- If the first subset ends in a 1, there is
 such subset and there are
such subset and there are  ways of making the second subset.
ways of making the second subset. - If the first subset ends in a 2, there is
 such subsets and there are
such subsets and there are  ways of making the second subset.
ways of making the second subset.
Thus, the number of combinations is  , and the probability again is
, and the probability again is ![]() .
.
See also
| 2001 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 5 |
Followed by Problem 7 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. 





 ways to arrange for values of
ways to arrange for values of  ways to arrange
ways to arrange  ways for this. We do not have to consider the order because the combination counts only one of the permutations; we can say that it counts the correct (ascending order) permutation.
ways for this. We do not have to consider the order because the combination counts only one of the permutations; we can say that it counts the correct (ascending order) permutation. ways to pick 3 numbers,
ways to pick 3 numbers,  ways to pick 2 numbers. We will duplicate both, so nothing else in this case matters.
ways to pick 2 numbers. We will duplicate both, so nothing else in this case matters. ways to pick 2 numbers. We pick one to duplicate with
ways to pick 2 numbers. We pick one to duplicate with  , so there are a total of 30 in this case.
, so there are a total of 30 in this case. ; all get duplicated so nothing else matters.
; all get duplicated so nothing else matters.



