Difference between revisions of "2003 AMC 12A Problems/Problem 13"
(→Solution) |
Danielguo94 (talk | contribs) (→See Also) |
||
| Line 23: | Line 23: | ||
== See Also == | == See Also == | ||
*[[2003 AMC 12A Problems]] | *[[2003 AMC 12A Problems]] | ||
| − | + | {{AMC12 box|year=2003|ab=A|num-b=12|num-a=14}} | |
| − | |||
[[Category:Introductory Geometry Problems]] | [[Category:Introductory Geometry Problems]] | ||
Revision as of 00:36, 28 April 2011
Problem
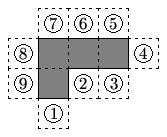
The polygon enclosed by the solid lines in the figure consists of 4 congruent squares joined edge-to-edge. One more congruent square is attatched to an edge at one of the nine positions indicated. How many of the nine resulting polygons can be folded to form a cube with one face missing?
![]()
Solution
Let the squares be labeled ![]() ,
, ![]() ,
, ![]() , and
, and ![]() .
.
When the polygon is folded, the "right" edge of square ![]() becomes adjacent to the "bottom edge" of square
becomes adjacent to the "bottom edge" of square ![]() , and the "bottom" edge of square
, and the "bottom" edge of square ![]() becomes adjacent to the "bottom" edge of square
becomes adjacent to the "bottom" edge of square ![]() .
.
So, any "new" square that is attatched to those edges will prevent the polygon from becoming a cube with one face missing.
Therefore, squares ![]() ,
, ![]() , and
, and ![]() will prevent the polygon from becoming a cube with one face missing.
will prevent the polygon from becoming a cube with one face missing.
Squares ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() will allow the polygon to become a cube with one face missing when folded.
will allow the polygon to become a cube with one face missing when folded.
Thus the answer is ![]() .
.
See Also
| 2003 AMC 12A (Problems • Answer Key • Resources) | |
| Preceded by Problem 12 |
Followed by Problem 14 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |