Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2003 AMC 12A Problems/Problem 15"

(→‎See Also)
Line 1: Line 1:
 +
{{duplicate|[[2003 AMC 12A Problems|2003 AMC 12A #15]] and [[2003 AMC 10A Problems|2003 AMC 10A #19]]}}
 
== Problem ==
 
== Problem ==
 
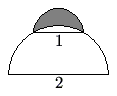
A [[semicircle]] of [[diameter]] <math>1</math> sits at the top of a semicircle of diameter <math>2</math>, as shown. The shaded [[area]] inside the smaller semicircle and outside the larger semicircle is called a ''lune''. Determine the area of this lune.  
 
A [[semicircle]] of [[diameter]] <math>1</math> sits at the top of a semicircle of diameter <math>2</math>, as shown. The shaded [[area]] inside the smaller semicircle and outside the larger semicircle is called a ''lune''. Determine the area of this lune.  
Line 19: Line 20:
 
The area of the triangle is <math>\frac{1^{2}\sqrt{3}}{4}=\frac{\sqrt{3}}{4}</math>
 
The area of the triangle is <math>\frac{1^{2}\sqrt{3}}{4}=\frac{\sqrt{3}}{4}</math>
  
−
So the shaded area is <math>\frac{1}{8}\pi-\frac{1}{6}\pi+\frac{\sqrt{3}}{4}=\frac{\sqrt{3}}{4}-\frac{1}{24}\pi \Rightarrow C</math>
+
So the shaded area is <math>\frac{1}{8}\pi-\frac{1}{6}\pi+\frac{\sqrt{3}}{4}=\boxed{\mathrm{(C)}\ \frac{\sqrt{3}}{4}-\frac{1}{24}\pi}</math>
  
 
== See Also ==
 
== See Also ==
−
*[[2003 AMC 12A Problems]]
+
{{AMC10 box|year=2003|ab=A|num-b=18|num-a=20}}
 
{{AMC12 box|year=2003|ab=A|num-b=14|num-a=16}}
 
{{AMC12 box|year=2003|ab=A|num-b=14|num-a=16}}
  
 
[[Category:Introductory Geometry Problems]]
 
[[Category:Introductory Geometry Problems]]

Revision as of 18:31, 31 July 2011

The following problem is from both the 2003 AMC 12A #15 and 2003 AMC 10A #19, so both problems redirect to this page.

Problem

A semicircle of diameter $1$ sits at the top of a semicircle of diameter $2$, as shown. The shaded area inside the smaller semicircle and outside the larger semicircle is called a lune. Determine the area of this lune.

2003amc10a19.gif

$\mathrm{(A) \ } \frac{1}{6}\pi-\frac{\sqrt{3}}{4}\qquad \mathrm{(B) \ } \frac{\sqrt{3}}{4}-\frac{1}{12}\pi\qquad \mathrm{(C) \ } \frac{\sqrt{3}}{4}-\frac{1}{24}\pi\qquad \mathrm{(D) \ } \frac{\sqrt{3}}{4}+\frac{1}{24}\pi\qquad \mathrm{(E) \ } \frac{\sqrt{3}}{4}+\frac{1}{12}\pi$

Solution

2003amc10a19solution.gif

The shaded area is equal to the area of the smaller semicircle minus the area of a sector of the larger circle plus the area of a triangle formed by two radii of the larger semicircle and the diameter of the smaller semicircle.

The area of the smaller semicircle is $\frac{1}{2}\pi\cdot(\frac{1}{2})^{2}=\frac{1}{8}\pi$.

Since the radius of the larger semicircle is equal to the diameter of the smaller semicircle, the triangle is an equilateral triangle and the sector measures $60^\circ$.

The area of the $60^\circ$ sector of the larger semicircle is $\frac{60}{360}\pi\cdot(\frac{2}{2})^{2}=\frac{1}{6}\pi$.

The area of the triangle is $\frac{1^{2}\sqrt{3}}{4}=\frac{\sqrt{3}}{4}$

So the shaded area is $\frac{1}{8}\pi-\frac{1}{6}\pi+\frac{\sqrt{3}}{4}=\boxed{\mathrm{(C)}\ \frac{\sqrt{3}}{4}-\frac{1}{24}\pi}$

See Also

2003 AMC 10A (Problems • Answer Key • Resources)
Preceded by
Problem 18 		Followed by
Problem 20
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions
2003 AMC 12A (Problems • Answer Key • Resources)
Preceded by
Problem 14 		Followed by
Problem 16
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions
Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2003_AMC_12A_Problems/Problem_15&oldid=41073"