Difference between revisions of "2003 AMC 12A Problems/Problem 17"
(→Solution 1) |
|||
| Line 14: | Line 14: | ||
<math>(x-2)^2 + y^2 = 2^2</math> | <math>(x-2)^2 + y^2 = 2^2</math> | ||
| + | Subtract the second equation from the first: | ||
| + | <math>x^2 + (y - 4)^2 - (x - 2)^2 - y^2 = 12</math> | ||
| − | + | <math>4x - 8y + 12 = 12</math> | |
| − | <math> | + | <math>x = 2y.</math> |
| − | <math> | + | Then substitute: |
| + | <math>(2y)^2 + (y - 4)^2 = 16</math> | ||
| − | <math>y^2 = | + | <math>4y^2 + y^2 - 8y + 16 = 16</math> |
| − | <math> | + | <math>5y^2 - 8y = 0</math> |
| + | <math>y(5y - 8) = 0.</math> | ||
| − | + | Thus <math>y = 0</math> and <math>y = \frac{8}{5}</math> making <math>x = 0</math> and <math>x = \frac{16}{5}</math>. | |
| − | + | The first value of <math>0</math> is obviously referring to the x-coordinate of the point where the circles intersect at the origin, <math>D</math>, so the second value must be referring to the x coordinate of <math>P</math>. Since <math>\overline{AD}</math> is the y-axis, the distance to it from <math>P</math> is the same as the x-value of the coordinate of <math>P</math>, so the distance from <math>P</math> to <math>\overline{AD}</math> is <math>\frac{16}{5} \Rightarrow B</math> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Solution 2== | ==Solution 2== | ||
Revision as of 13:02, 14 February 2014
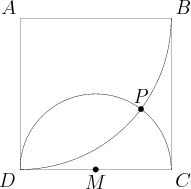
Problem
Square ![]() has sides of length
has sides of length ![]() , and
, and ![]() is the midpoint of
is the midpoint of ![]() . A circle with radius
. A circle with radius ![]() and center
and center ![]() intersects a circle with radius
intersects a circle with radius ![]() and center
and center ![]() at points
at points ![]() and
and ![]() . What is the distance from
. What is the distance from ![]() to
to ![]() ?
?
![]()
Solution 1
Let ![]() be the origin.
be the origin. ![]() is the point
is the point ![]() and
and ![]() is the point
is the point ![]() . We are given the radius of the quarter circle and semicircle as
. We are given the radius of the quarter circle and semicircle as ![]() and
and ![]() , respectively, so their equations, respectively, are:
, respectively, so their equations, respectively, are:
![]()
![]()
Subtract the second equation from the first:
![]()
![]()
![]()
Then substitute:
![]()
![]()
![]()
![]()
Thus ![]() and
and ![]() making
making ![]() and
and ![]() .
.
The first value of ![]() is obviously referring to the x-coordinate of the point where the circles intersect at the origin,
is obviously referring to the x-coordinate of the point where the circles intersect at the origin, ![]() , so the second value must be referring to the x coordinate of
, so the second value must be referring to the x coordinate of ![]() . Since
. Since ![]() is the y-axis, the distance to it from
is the y-axis, the distance to it from ![]() is the same as the x-value of the coordinate of
is the same as the x-value of the coordinate of ![]() , so the distance from
, so the distance from ![]() to
to ![]() is
is ![]()
Solution 2
Note that ![]() is merely a reflection of
is merely a reflection of ![]() over
over ![]() . Call the intersection of
. Call the intersection of ![]() and
and ![]()
![]() . Drop perpendiculars from
. Drop perpendiculars from ![]() and
and ![]() to
to ![]() , and denote their respective points of intersection by
, and denote their respective points of intersection by ![]() and
and ![]() . We then have
. We then have ![]() , with a scale factor of 2. Thus, we can find
, with a scale factor of 2. Thus, we can find ![]() and double it to get our answer. With some analytical geometry, we find that
and double it to get our answer. With some analytical geometry, we find that ![]() , implying that
, implying that ![]() .
.
Solution 3
As in Solution 2, draw in ![]() and
and ![]() and denote their intersection point
and denote their intersection point ![]() . Next, drop a perpendicular from
. Next, drop a perpendicular from ![]() to
to ![]() and denote the foot as
and denote the foot as ![]() .
. ![]() as they are both radii and similarly
as they are both radii and similarly ![]() so
so ![]() is a kite and
is a kite and ![]() by a well-known theorem.
by a well-known theorem.
Pythagorean theorem gives us ![]() . Clearly
. Clearly ![]() by angle-angle and
by angle-angle and ![]() by Hypotenuse Leg.
Manipulating similar triangles gives us
by Hypotenuse Leg.
Manipulating similar triangles gives us ![]()
See Also
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.