2004 AIME I Problems/Problem 10
Problem
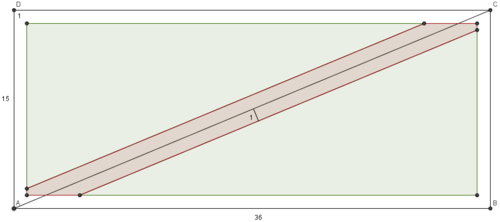
A circle of radius 1 is randomly placed in a 15-by-36 rectangle ![]() so that the circle lies completely within the rectangle. Given that the probability that the circle will not touch diagonal
so that the circle lies completely within the rectangle. Given that the probability that the circle will not touch diagonal ![]() is
is ![]() where
where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]()
Solution
Solution 1
Solution 2
The location of the center of the circle must be in the ![]() rectangle that is one unit away from the sides of rectangle
rectangle that is one unit away from the sides of rectangle ![]() . We want to find the area of the right triangle with hypotenuse one unit away from
. We want to find the area of the right triangle with hypotenuse one unit away from ![]() .
.
Let ![]() be at the origin,
be at the origin, ![]() at
at ![]() ,
, ![]() at
at ![]() ,
, ![]() at
at ![]() . The slope of diagonal
. The slope of diagonal ![]() is
is ![]() . Since the hypotenuse is parallel to the diagonal, it has the same slope, and its equation is
. Since the hypotenuse is parallel to the diagonal, it has the same slope, and its equation is ![]() . Manipulating,
. Manipulating, ![]() . We need to find the value of
. We need to find the value of ![]() , which can be determined using the fact that the hypotenuse is one unit away from the diagonal. Since the diagonal contains the origin, we can use the distance from a point to the line formula at the origin:
, which can be determined using the fact that the hypotenuse is one unit away from the diagonal. Since the diagonal contains the origin, we can use the distance from a point to the line formula at the origin:
![]()
![\[\left|\frac{(5)(0) + (-12)(0) + 12c}{\sqrt{5^2 + (-12)^2}}\right| = 1\]](http://latex.artofproblemsolving.com/6/5/5/6550101f7f5e01a655563120d0a6f0e602312adf.png)
![]()
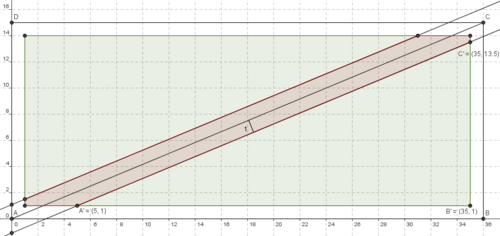
It makes sense that we have two values of ![]() , one for the triangle on top of the diagonal, and one for the bottom. We will just consider the bottom triangle, so
, one for the triangle on top of the diagonal, and one for the bottom. We will just consider the bottom triangle, so ![]() . Then the equation of the line is
. Then the equation of the line is ![]() . Solving for its intersections with the lines
. Solving for its intersections with the lines ![]() we find the coordinates of the triangles are at
we find the coordinates of the triangles are at ![]() . The area is
. The area is ![]() .
.
Finally, the probability is ![]() , and
, and ![]() .
.
See also
| 2004 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 9 |
Followed by Problem 11 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||