Difference between revisions of "2004 AMC 12A Problems/Problem 22"
Aopssolver1 (talk | contribs) (→See also) |
(Created higher-quality images) |
||
| Line 9: | Line 9: | ||
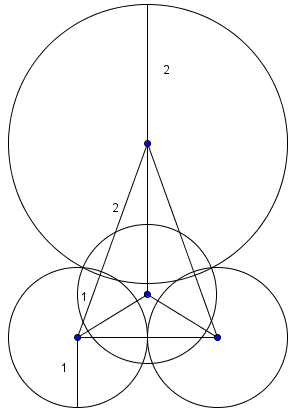
We draw the three spheres of radius <math>1</math>: | We draw the three spheres of radius <math>1</math>: | ||
| − | [[File: | + | [[File:2004AMC12A_22_1_rerender.png]] |
And then add the sphere of radius <math>2</math>: | And then add the sphere of radius <math>2</math>: | ||
| − | [[File: | + | [[File:2004AMC12A_22_2_rerender.png]] |
The height from the center of the bottom sphere to the plane is <math>1</math>, and from the center of the top sphere to the tip is <math>2</math>. | The height from the center of the bottom sphere to the plane is <math>1</math>, and from the center of the top sphere to the tip is <math>2</math>. | ||
Revision as of 14:12, 17 January 2016
- The following problem is from both the 2004 AMC 12A #22 and 2004 AMC 10A #25, so both problems redirect to this page.
Problem
Three mutually tangent spheres of radius ![]() rest on a horizontal plane. A sphere of radius
rest on a horizontal plane. A sphere of radius ![]() rests on them. What is the distance from the plane to the top of the larger sphere?
rests on them. What is the distance from the plane to the top of the larger sphere?
![]()
Solution
We draw the three spheres of radius ![]() :
:
And then add the sphere of radius ![]() :
:
The height from the center of the bottom sphere to the plane is ![]() , and from the center of the top sphere to the tip is
, and from the center of the top sphere to the tip is ![]() .
.
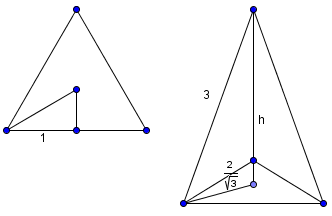
We now need the vertical height of the centers. If we connect the centers, we get a triangular pyramid with an equilateral triangle base. The distance from the vertex of the equilateral triangle to its centroid can be found by ![]() s to be
s to be ![]() .
.
By the Pythagorean Theorem, we have ![]() . Adding the heights up, we get
. Adding the heights up, we get 
See also
| 2004 AMC 12A (Problems • Answer Key • Resources) | |
| Preceded by Problem 21 |
Followed by Problem 23 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
| 2004 AMC 10A (Problems • Answer Key • Resources) | ||
| Preceded by Problem 24 |
Followed by Last Question | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.