Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2005 AIME I Problems/Problem 1"

(Image Added)
m (fix error (noted by JBL))
Line 1: Line 1:
 
== Problem ==
 
== Problem ==
−
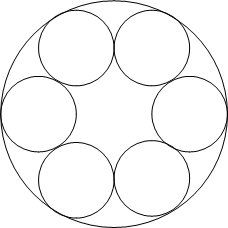
Six [[circle]]s form a ring with with each circle [[externally tangent]] to two circles adjacent to it. All circles are [[internally tangent]] to a circle <math> C </math> with [[radius]] 30. Let <math> K </math> be the area of the region inside circle <math> C </math> and outside of the six circles in the ring. Find <math> \lfloor K \rfloor</math> (the [[floor function]]).
+
Six [[congruent]] [[circle]]s form a ring with with each circle [[externally tangent]] to two circles adjacent to it. All circles are [[internally tangent]] to a circle <math> C </math> with [[radius]] 30. Let <math> K </math> be the area of the region inside circle <math> C </math> and outside of the six circles in the ring. Find <math> \lfloor K \rfloor</math> (the [[floor function]]).
  
 
[[Image:2005 AIME I Problem 1.png]]
 
[[Image:2005 AIME I Problem 1.png]]
Line 9: Line 9:
 
== See also ==
 
== See also ==
 
{{AIME box|year=2005|n=I|before=First Question|num-a=2}}
 
{{AIME box|year=2005|n=I|before=First Question|num-a=2}}
 +
 +
[[Category:Intermediate Geometry Problems]]

Revision as of 14:13, 2 December 2007

Problem

Six congruent circles form a ring with with each circle externally tangent to two circles adjacent to it. All circles are internally tangent to a circle $C$ with radius 30. Let $K$ be the area of the region inside circle $C$ and outside of the six circles in the ring. Find $\lfloor K \rfloor$ (the floor function).

2005 AIME I Problem 1.png

Solution

Define the radii of the six congruent circles as $r$. If we draw all of the radii to the points of external tangency, we get a regular hexagon. If we connect the vertices of the hexagon to the center of the circle $C$, we form several equilateral triangles. The length of each side of the triangle is $2r$. Notice that the radius of circle $C$ is equal to the length of the side of the triangle plus $r$. Thus, the radius of $C$ has a length of $3r = 30$, and so $r = 10$. $K = 30^2\pi - 6(10^2\pi) = 300\pi$, so $\lfloor 300\pi \rfloor = 942$.

See also

2005 AIME I (Problems • Answer Key • Resources)
Preceded by
First Question 		Followed by
Problem 2
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions
Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2005_AIME_I_Problems/Problem_1&oldid=20523"