Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2005 AMC 10A Problems/Problem 19"

(→‎Solution Add-On)
(→‎Solution)
 
Line 25: Line 25:
 
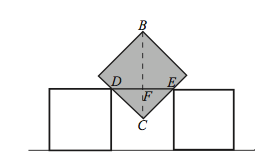
Consider the rotated middle square shown in the figure. It will drop until length <math>DE</math> is 1 inch. Then, because <math>DEC</math> is a <math>45^{\circ}-45^{\circ}-90^{\circ}</math> triangle, <math>EC=\frac{\sqrt{2}}{2}</math>, and <math>FC=\frac{1}{2}</math>. We know that <math>BC=\sqrt{2}</math>, so the distance from <math>B</math> to the line is  
 
Consider the rotated middle square shown in the figure. It will drop until length <math>DE</math> is 1 inch. Then, because <math>DEC</math> is a <math>45^{\circ}-45^{\circ}-90^{\circ}</math> triangle, <math>EC=\frac{\sqrt{2}}{2}</math>, and <math>FC=\frac{1}{2}</math>. We know that <math>BC=\sqrt{2}</math>, so the distance from <math>B</math> to the line is  
  
−
<math>BC-FC+1=\sqrt{2}-\frac{1}{2}+1=\sqrt{2}+\dfrac{1}{2}</math> <math>(D)</math>.
+
<math>BC-FC+1=\sqrt{2}-\frac{1}{2}+1=\boxed{\textbf{(D) }\sqrt{2}+\dfrac{1}{2}}</math>.
  
 
[[File:AMC10200519Sol.png]]
 
[[File:AMC10200519Sol.png]]
Line 36: Line 36:
 
After deducing that <math>BC=\sqrt{2}</math>, we can observe that the length from <math>C</math> to the baseline is <math>\frac{1}{2}</math>. This can be obtained by subtracting <math>FC</math> from the side length of the square(s), which is <math>1</math>.
 
After deducing that <math>BC=\sqrt{2}</math>, we can observe that the length from <math>C</math> to the baseline is <math>\frac{1}{2}</math>. This can be obtained by subtracting <math>FC</math> from the side length of the square(s), which is <math>1</math>.
  
−
Adding these up, we see that our answer is <math>(D)</math> <math>\sqrt{2}+\dfrac{1}{2}</math>.
+
Adding these up, we see that our answer is <math>\boxed{\textbf{(D) }\sqrt{2}+\dfrac{1}{2}}</math>.
  
−
sdk652
+
- sdk652
  
 
==See Also==
 
==See Also==

Latest revision as of 12:46, 14 December 2021

Problem

Three one-inch squares are placed with their bases on a line. The center square is lifted out and rotated 45 degrees, as shown. Then it is centered and lowered into its original location until it touches both of the adjoining squares. How many inches is the point $B$ from the line on which the bases of the original squares were placed?

[asy] unitsize(1inch); defaultpen(linewidth(.8pt)+fontsize(8pt)); draw((0,0)--((1/3) + 3*(1/2),0)); fill(((1/6) + (1/2),0)--((1/6) + (1/2),(1/2))--((1/6) + 1,(1/2))--((1/6) + 1,0)--cycle, rgb(.7,.7,.7)); draw(((1/6),0)--((1/6) + (1/2),0)--((1/6) + (1/2),(1/2))--((1/6),(1/2))--cycle); draw(((1/6) + (1/2),0)--((1/6) + (1/2),(1/2))--((1/6) + 1,(1/2))--((1/6) + 1,0)--cycle); draw(((1/6) + 1,0)--((1/6) + 1,(1/2))--((1/6) + (3/2),(1/2))--((1/6) + (3/2),0)--cycle); draw((2,0)--(2 + (1/3) + (3/2),0)); draw(((2/3) + (3/2),0)--((2/3) + 2,0)--((2/3) + 2,(1/2))--((2/3) + (3/2),(1/2))--cycle); draw(((2/3) + (5/2),0)--((2/3) + (5/2),(1/2))--((2/3) + 3,(1/2))--((2/3) + 3,0)--cycle); label("$B$",((1/6) + (1/2),(1/2)),NW); label("$B$",((2/3) + 2 + (1/4),(29/30)),NNE); draw(((1/6) + (1/2),(1/2)+0.05)..(1,.8)..((2/3) + 2 + (1/4)-.05,(29/30)),EndArrow(HookHead,3)); fill(((2/3) + 2 + (1/4),(1/4))--((2/3) + (5/2) + (1/10),(1/2) + (1/9))--((2/3) + 2 + (1/4),(29/30))--((2/3) + 2 - (1/10),(1/2) + (1/9))--cycle, rgb(.7,.7,.7)); draw(((2/3) + 2 + (1/4),(1/4))--((2/3) + (5/2) + (1/10),(1/2) + (1/9))--((2/3) + 2 + (1/4),(29/30))--((2/3) + 2 - (1/10),(1/2) + (1/9))--cycle);[/asy]

$\textbf{(A)}\ 1\qquad\textbf{(B)}\ \sqrt{2}\qquad\textbf{(C)}\ \frac{3}{2}\qquad\textbf{(D)}\ \sqrt{2}+\frac{1}{2}\qquad\textbf{(E)}\ 2$

Solution

Consider the rotated middle square shown in the figure. It will drop until length $DE$ is 1 inch. Then, because $DEC$ is a $45^{\circ}-45^{\circ}-90^{\circ}$ triangle, $EC=\frac{\sqrt{2}}{2}$, and $FC=\frac{1}{2}$. We know that $BC=\sqrt{2}$, so the distance from $B$ to the line is

$BC-FC+1=\sqrt{2}-\frac{1}{2}+1=\boxed{\textbf{(D) }\sqrt{2}+\dfrac{1}{2}}$.

AMC10200519Sol.png


Note

(Refer to Diagram Above)

After deducing that $BC=\sqrt{2}$, we can observe that the length from $C$ to the baseline is $\frac{1}{2}$. This can be obtained by subtracting $FC$ from the side length of the square(s), which is $1$.

Adding these up, we see that our answer is $\boxed{\textbf{(D) }\sqrt{2}+\dfrac{1}{2}}$.

- sdk652

See Also

2005 AMC 10A (Problems • Answer Key • Resources)
Preceded by
Problem 18 		Followed by
Problem 20
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2005_AMC_10A_Problems/Problem_19&oldid=167684"