Difference between revisions of "2005 AMC 10A Problems/Problem 8"
(→Solution) |
|||
| Line 7: | Line 7: | ||
==Solution== | ==Solution== | ||
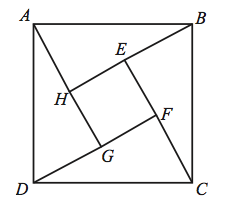
| − | + | We see that side <math>BE</math>, which we know is 1, is also the shorter leg of one of the four right triangles (which are congruent, I'll not prove this). So, <math>AH = 1</math>. Then <math>HB = HE + BE = HE + 1</math>, and <math>HE</math> is one of the sides of the square whose area we want to find. So: | |
<math>1^2 + (HE+1)^2=\sqrt{50}^2</math> | <math>1^2 + (HE+1)^2=\sqrt{50}^2</math> | ||
| Line 17: | Line 17: | ||
<math>HE+1=7</math> | <math>HE+1=7</math> | ||
| − | <math>HE=6</math> So, the area of the square is <math>6^2=\boxed{36}</math>. | + | <math>HE=6</math> So, the area of the square is <math>6^2=\boxed{36} \rightarrow (C)</math>. |
==See Also== | ==See Also== | ||
Revision as of 22:35, 3 January 2016
Problem
In the figure, the length of side ![]() of square
of square ![]() is
is ![]() and
and ![]() =1. What is the area of the inner square
=1. What is the area of the inner square ![]() ?
?
![]()
Solution
We see that side ![]() , which we know is 1, is also the shorter leg of one of the four right triangles (which are congruent, I'll not prove this). So,
, which we know is 1, is also the shorter leg of one of the four right triangles (which are congruent, I'll not prove this). So, ![]() . Then
. Then ![]() , and
, and ![]() is one of the sides of the square whose area we want to find. So:
is one of the sides of the square whose area we want to find. So:
![]()
![]()
![]()
![]()
![]() So, the area of the square is
So, the area of the square is ![]() .
.
See Also
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.