Difference between revisions of "2005 PMWC Problems/Problem T8"
m (→Solution) |
m (→Solution) |
||
| (One intermediate revision by one other user not shown) | |||
| Line 1: | Line 1: | ||
== Problem == | == Problem == | ||
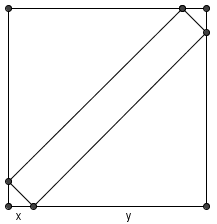
| − | An [[isosceles triangle|isosceles]] [[right triangle]] is removed from each corner of a [[square]] piece of paper so that a [[rectangle]] of unequal sides remains. If the sum of the areas of the cut-off pieces is | + | An [[isosceles triangle|isosceles]] [[right triangle]] is removed from each corner of a [[square]] piece of paper so that a [[rectangle]] of unequal sides remains. If the sum of the areas of the cut-off pieces is <math>200</math> and the lengths of the legs of the triangles cut off are integers, find the area of the rectangle. |
== Solution == | == Solution == | ||
| − | |||
| − | Since the figure in the middle is a rectangle, the isosceles triangles on opposite vertices are congruent. Let <math>x</math> be | + | Since the figure in the middle is a rectangle, the isosceles triangles on opposite vertices are congruent. Let <math>x</math> be the leg of the smaller triangles, and <math>y</math> be the leg of the other two. The sum of the areas of the triangle is then <math>2\left(\frac{1}{2}x^2\right) + 2\left(\frac{1}{2}y^2\right) = x^2 + y^2 = 200</math>. (Remember that the sides are of unequal lengths, so we exclude <math>x = y= 10</math>). Since squares <math>\equiv 0,1 \pmod{4}</math>, we can reduce our search to even integers, and a short bit of trial and error yield <math>x = 2, y = 14</math> works. |
| + | |||
| + | Using subtraction of areas or <math>45-45-90</math> triangles, we find that the area of the rectangle is <math>(x + y)^2 - x^2 - y^2 = 2xy</math>; so the area of the rectangle is <math>2(2)(14) = 56</math>. | ||
| − | + | [[Image:2005_PMWC-T8.png]] | |
== See also == | == See also == | ||
{{PMWC box|year=2005|num-b=T7|num-a=T9}} | {{PMWC box|year=2005|num-b=T7|num-a=T9}} | ||
Latest revision as of 22:58, 1 January 2020
Problem
An isosceles right triangle is removed from each corner of a square piece of paper so that a rectangle of unequal sides remains. If the sum of the areas of the cut-off pieces is ![]() and the lengths of the legs of the triangles cut off are integers, find the area of the rectangle.
and the lengths of the legs of the triangles cut off are integers, find the area of the rectangle.
Solution
Since the figure in the middle is a rectangle, the isosceles triangles on opposite vertices are congruent. Let ![]() be the leg of the smaller triangles, and
be the leg of the smaller triangles, and ![]() be the leg of the other two. The sum of the areas of the triangle is then
be the leg of the other two. The sum of the areas of the triangle is then ![]() . (Remember that the sides are of unequal lengths, so we exclude
. (Remember that the sides are of unequal lengths, so we exclude ![]() ). Since squares
). Since squares ![]() , we can reduce our search to even integers, and a short bit of trial and error yield
, we can reduce our search to even integers, and a short bit of trial and error yield ![]() works.
works.
Using subtraction of areas or ![]() triangles, we find that the area of the rectangle is
triangles, we find that the area of the rectangle is ![]() ; so the area of the rectangle is
; so the area of the rectangle is ![]() .
.
See also
| 2005 PMWC (Problems) | ||
| Preceded by Problem T7 |
Followed by Problem T9 | |
| I: 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 T: 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 | ||