Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2006 AIME I Problems/Problem 1"

(→‎Problem)
(→‎Solution)
Line 3: Line 3:
  
 
== Solution ==
 
== Solution ==
−
From the problem statement, we construct the following diagram: <div style="text-align:center">[[Image:Aime06i.1.PNG]]</div>
 
  
−
Using the [[Pythagorean Theorem]]:
+
Let the side length be called <math>x</math>.
 +
[[Image:Diagram1.png]]
  
−
<div style="text-align:center"><math> (AD)^2 = (AC)^2 + (CD)^2 </math></div>
+
Then <math>AB=BC=CD=DE=EF=AF=x</math>.
  
−
<div style="text-align:center"><math> (AC)^2 = (AB)^2 + (BC)^2 </math></div>
+
The diagonal <math>BF=\sqrt{AB^2+AF^2}=\sqrt{x^2+x^2}=x\sqrt{2}</math>.
  
−
Substituting <math>(AB)^2 + (BC)^2 </math> for <math> (AC)^2 </math>:
+
Then the areas of the triangles AFB and CDE in total are <math>\frac{x^2}{2}\cdot 2</math>,
 +
and the area of the rectangle BCEF equals <math>x\cdot x\sqrt{2}=x^2\sqrt{2}</math>
  
−
<div style="text-align:center"><math> (AD)^2 = (AB)^2 + (BC)^2 + (CD)^2 </math></div>
+
Then we have to solve the equation
  
−
Plugging in the given information:
+
<math>2116(\sqrt{2}+1)=x^2\sqrt{2}+x^2</math>.
  
−
<div style="text-align:center"><math> (AD)^2 = (18)^2 + (21)^2 + (14)^2 </math></div>
+
<math>2116(\sqrt{2}+1)=x^2(\sqrt{2}+1)</math>
  
−
<div style="text-align:center"><math> (AD)^2 = 961 </math></div>
+
<math>2116=x^2</math>
  
−
<div style="text-align:center"><math> (AD)= 31 </math></div>
+
<math>x=46</math>
  
−
So the perimeter is <math> 18+21+14+31=84 </math>, and the answer is <math>084</math>.
+
Therefore, AB is 46.
  
 
== See also ==
 
== See also ==

Revision as of 13:54, 25 September 2007

Problem

In convex hexagon $ABCDEF$, all six sides are congruent, $\angle A$ and $\angle D$ are right angles, and $\angle B, \angle C, \angle E,$ and $\angle F$ are congruent. The area of the hexagonal region is $2116(\sqrt{2}+1).$ Find $AB$.

Solution

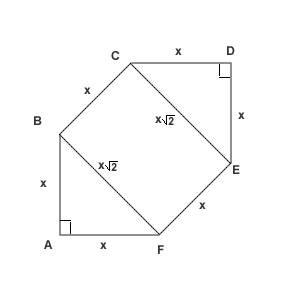
Let the side length be called $x$. Diagram1.png

Then $AB=BC=CD=DE=EF=AF=x$.

The diagonal $BF=\sqrt{AB^2+AF^2}=\sqrt{x^2+x^2}=x\sqrt{2}$.

Then the areas of the triangles AFB and CDE in total are $\frac{x^2}{2}\cdot 2$, and the area of the rectangle BCEF equals $x\cdot x\sqrt{2}=x^2\sqrt{2}$

Then we have to solve the equation

$2116(\sqrt{2}+1)=x^2\sqrt{2}+x^2$.

$2116(\sqrt{2}+1)=x^2(\sqrt{2}+1)$

$2116=x^2$

$x=46$

Therefore, AB is 46.

See also

2006 AIME I (Problems • Answer Key • Resources)
Preceded by
First Question 		Followed by
Problem 2
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions
Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2006_AIME_I_Problems/Problem_1&oldid=16791"