2006 AMC 10B Problems/Problem 15
Revision as of 15:01, 2 August 2006 by Xantos C. Guin (talk | contribs) (added link to previous and next problem)
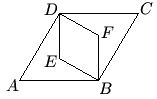
Problem
Rhombus ![]() is similar to rhombus
is similar to rhombus ![]() . The area of rhombus
. The area of rhombus ![]() is
is ![]() and
and ![]() . What is the area of rhombus
. What is the area of rhombus ![]() ?
?
![]()
Solution
Using properties of a rhombus:
![]() .
.
![]() .
.
It is easy to see that rhombus ![]() is made up of equilateral triangles
is made up of equilateral triangles ![]() and
and ![]() .
.
Let the lengths of the sides of rhombus ![]() be
be ![]() .
.
The longer diagonal of rhombus ![]() is
is ![]() . Since
. Since ![]() is a side of an equilateral triangle with a side length of
is a side of an equilateral triangle with a side length of ![]() ,
, ![]() .
.
The longer diagonal of rhombus ![]() is
is ![]() . Since
. Since ![]() is twice the length of an altitude of of an equilateral triangle with a side length of
is twice the length of an altitude of of an equilateral triangle with a side length of ![]() ,
, ![]()
The ratio of the longer diagonal of rhombus ![]() to rhombus
to rhombus ![]() is
is ![]()
Therefore, the ratio of the area of rhombus ![]() to rhombus
to rhombus ![]() is
is 
Let ![]() be the area of rhombus
be the area of rhombus ![]() .
.
![]()
![]()