Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2006 AMC 10B Problems/Problem 19"

(Added problem and solution)
m (proofreading)
Line 8: Line 8:
  
 
== Solution ==
 
== Solution ==
−
The shaded area is equivilant to the area of sector <math>DOE</math> minus the area of triangle <math>DOE</math> plus the area of triangle <math>DBE</math>.  
+
The shaded area is equivilant to the area of sector <math>DOE</math>, minus the area of triangle <math>DOE</math> plus the area of triangle <math>DBE</math>.  
  
 
Using the Pythagorean Theorem:  
 
Using the Pythagorean Theorem:  
Line 16: Line 16:
 
<math>DA=CE=\sqrt{3}</math>
 
<math>DA=CE=\sqrt{3}</math>
  
−
Clearly <math>DOA</math> and <math>EOC</math> are <math>30-60-90</math> triangles with <math>\angle EOC = \angle DOA = 60^\circ </math>
+
Clearly, <math>DOA</math> and <math>EOC</math> are <math>30-60-90</math> triangles with <math>\angle EOC = \angle DOA = 60^\circ </math>.
  
−
Since <math>OABC</math> is a square, <math> \angle COA = 90^\circ </math>
+
Since <math>OABC</math> is a square, <math> \angle COA = 90^\circ </math>.
  
 
<math>\angle DOE</math> can be found by doing some subtraction of angles.  
 
<math>\angle DOE</math> can be found by doing some subtraction of angles.  
Line 30: Line 30:
 
<math>  60^\circ - 30^\circ = \angle DOE = 30^\circ </math>
 
<math>  60^\circ - 30^\circ = \angle DOE = 30^\circ </math>
  
−
So the area of sector <math>DOE</math> is <math> \frac{30}{360} \cdot \pi \cdot 2^2 = \frac{\pi}{3} </math>
+
So, the area of sector <math>DOE</math> is <math> \frac{30}{360} \cdot \pi \cdot 2^2 = \frac{\pi}{3} </math>.
  
−
The area of triangle <math>DOE</math> is <math> \frac{1}{2}\cdot 2 \cdot 2 \cdot \sin 30^\circ = 1 </math>
+
The area of triangle <math>DOE</math> is <math> \frac{1}{2}\cdot 2 \cdot 2 \cdot \sin 30^\circ = 1 </math>.
  
−
Since <math>AB=CB=1</math> , <math>DB=ED=(\sqrt{3}-1)</math>  
+
Since <math>AB=CB=1</math> , <math>DB=ED=(\sqrt{3}-1)</math>.
  
−
So the area of triangle <math>DBE</math> is <math>\frac{1}{2} \cdot (\sqrt{3}-1)^2 = 2-\sqrt{3}</math>  
+
So, the area of triangle <math>DBE</math> is <math>\frac{1}{2} \cdot (\sqrt{3}-1)^2 = 2-\sqrt{3}</math>.
  
 
Therefore, the shaded area is <math> (\frac{\pi}{3}) - (1) + (2-\sqrt{3}) = \frac{\pi}{3}+1-\sqrt{3} \Rightarrow A </math>
 
Therefore, the shaded area is <math> (\frac{\pi}{3}) - (1) + (2-\sqrt{3}) = \frac{\pi}{3}+1-\sqrt{3} \Rightarrow A </math>

Revision as of 13:30, 18 July 2006

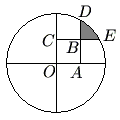
Problem

A circle of radius $2$ is centered at $O$. Square $OABC$ has side length $1$. Sides $AB$ and $CB$ are extended past $B$ to meet the circle at $D$ and $E$, respectively. What is the area of the shaded region in the figure, which is bounded by $BD$, $BE$, and the minor arc connecting $D$ and $E$?

2006amc10b19.gif

$\mathrm{(A) \ } \frac{\pi}{3}+1-\sqrt{3}\qquad \mathrm{(B) \ } \frac{\pi}{2}(2-\sqrt{3}) \qquad \mathrm{(C) \ } \pi(2-\sqrt{3})\qquad \mathrm{(D) \ } \frac{\pi}{6}+\frac{\sqrt{3}+1}{2}\qquad \mathrm{(E) \ } \frac{\pi}{3}-1+\sqrt{3}$

Solution

The shaded area is equivilant to the area of sector $DOE$, minus the area of triangle $DOE$ plus the area of triangle $DBE$.

Using the Pythagorean Theorem:

$(DA)^2=(CE)^2=2^2-1^2=3$

$DA=CE=\sqrt{3}$

Clearly, $DOA$ and $EOC$ are $30-60-90$ triangles with $\angle EOC = \angle DOA = 60^\circ$.

Since $OABC$ is a square, $\angle COA = 90^\circ$.

$\angle DOE$ can be found by doing some subtraction of angles.

$\angle COA - \angle DOA = \angle EOA$

$90^\circ - 60^\circ = \angle EOA = 30^\circ$

$\angle DOA - \angle EOA = \angle DOE$

$60^\circ - 30^\circ = \angle DOE = 30^\circ$

So, the area of sector $DOE$ is $\frac{30}{360} \cdot \pi \cdot 2^2 = \frac{\pi}{3}$.

The area of triangle $DOE$ is $\frac{1}{2}\cdot 2 \cdot 2 \cdot \sin 30^\circ = 1$.

Since $AB=CB=1$ , $DB=ED=(\sqrt{3}-1)$.

So, the area of triangle $DBE$ is $\frac{1}{2} \cdot (\sqrt{3}-1)^2 = 2-\sqrt{3}$.

Therefore, the shaded area is $(\frac{\pi}{3}) - (1) + (2-\sqrt{3}) = \frac{\pi}{3}+1-\sqrt{3} \Rightarrow A$

See Also

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2006_AMC_10B_Problems/Problem_19&oldid=7893"