Difference between revisions of "2006 Cyprus MO/Lyceum/Problem 17"
(solution) |
m (→Problem) |
||
| (4 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
==Problem== | ==Problem== | ||
| − | + | [[Image:2006 CyMO-17.PNG|250px|right]] | |
| − | [[Image:2006 CyMO-17.PNG|250px]] | ||
| − | |||
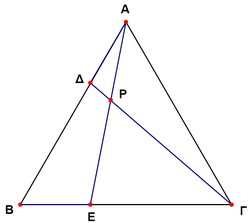
| − | <math> | + | <math>AB\Gamma</math> is equilateral triangle of side <math>\alpha</math> and <math>A\Delta=BE=\frac{\alpha}{3}</math>. The measure of the angle <math>\angle\Gamma PE</math> is |
| − | + | <math>\mathrm{(A)}\ 60^\circ\qquad\mathrm{(B)}\ 50^\circ\qquad\mathrm{(C)}\ 40^\circ\qquad\mathrm{(D)}\ 45^\circ\qquad\mathrm{(E)}\ 70^\circ</math> | |
| − | + | ==Solution== | |
| + | Label point <math>F</math> on <math>A\Gamma</math> such that <math>\Gamma F=\frac{\alpha}{3}</math>. | ||
| − | + | By symmetry we see that the triangle in the middle is equilateral, so the measure of <math>\angle\Gamma PE</math> is <math>60^{\circ}</math>, and the answer is <math>\mathrm{(A)}</math>. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==See also== | ==See also== | ||
Latest revision as of 22:00, 30 November 2015
Problem
is equilateral triangle of side 
and 
. The measure of the angle 
is
Solution
Label point 
on 
such that 
.
By symmetry we see that the triangle in the middle is equilateral, so the measure of is 
, and the answer is 
.
See also
| 2006 Cyprus MO, Lyceum (Problems) | ||
| Preceded by Problem 16 |
Followed by Problem 18 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 • 26 • 27 • 28 • 29 • 30 | ||
