2007 AIME II Problems/Problem 13
Problem
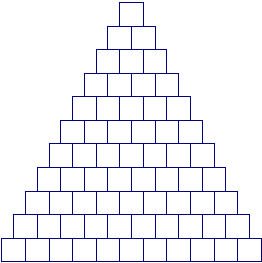
A triangular array of squares has one square in the first row, two in the second, and in general, ![]() squares in the
squares in the ![]() th row for
th row for ![]() With the exception of the bottom row, each square rests on two squares in the row immediately below (illustrated in given diagram). In each square of the eleventh row, a
With the exception of the bottom row, each square rests on two squares in the row immediately below (illustrated in given diagram). In each square of the eleventh row, a ![]() or a
or a ![]() is placed. Numbers are then placed into the other squares, with the entry for each square being the sum of the entries in the two squares below it. For how many initial distributions of
is placed. Numbers are then placed into the other squares, with the entry for each square being the sum of the entries in the two squares below it. For how many initial distributions of ![]() 's and
's and ![]() 's in the bottom row is the number in the top square a multiple of
's in the bottom row is the number in the top square a multiple of ![]() ?
?
Solution
Label each of the bottom squares as ![]() .
.
Through induction, we can find that the top square is equal to  . (This also makes sense based on a combinatorial argument: the number of ways a number can "travel" to the top position going only up is equal to the number of times it will be counted in the final sum.)
. (This also makes sense based on a combinatorial argument: the number of ways a number can "travel" to the top position going only up is equal to the number of times it will be counted in the final sum.)
Examine the equation ![]() . All of the coefficients from
. All of the coefficients from ![]() will be multiples of
will be multiples of ![]() (since the numerator will have a
(since the numerator will have a ![]() ). Thus, the expression boils down to
). Thus, the expression boils down to ![]() . Reduce to find that
. Reduce to find that ![]() . Out of
. Out of ![]() , either all are equal to
, either all are equal to ![]() , or three of them are equal to
, or three of them are equal to ![]() . This gives
. This gives  possible combinations of numbers that work.
possible combinations of numbers that work.
The seven terms from ![]() can assume either
can assume either ![]() or
or ![]() , giving us
, giving us ![]() possibilities. The answer is therefore
possibilities. The answer is therefore ![]() .
.
See also
| 2007 AIME II (Problems • Answer Key • Resources) | ||
| Preceded by Problem 12 |
Followed by Problem 14 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||