Difference between revisions of "2007 AIME II Problems/Problem 3"
(add solution) |
|||
| Line 5: | Line 5: | ||
== Solution == | == Solution == | ||
| + | |||
| + | |||
| + | == '''Solution 1.''' == | ||
| + | |||
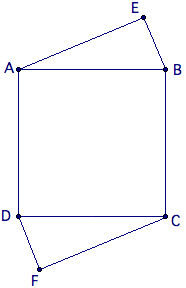
Extend <math>\overline{AE}, \overline{DF}</math> and <math>\overline{BE}, \overline{CF}</math> to their points of intersection. Since <math>\triangle ABE \cong \triangle CDF</math> and are both <math>5-12-13</math> [[right triangle]]s, we can come to the conclusion that the two new triangles are also congruent to these two (use [[ASA]], as we know all the sides are <math>13</math> and the angles are mostly complementary). Thus, we create a [[square]] with sides <math>5 + 12 = 17</math>. | Extend <math>\overline{AE}, \overline{DF}</math> and <math>\overline{BE}, \overline{CF}</math> to their points of intersection. Since <math>\triangle ABE \cong \triangle CDF</math> and are both <math>5-12-13</math> [[right triangle]]s, we can come to the conclusion that the two new triangles are also congruent to these two (use [[ASA]], as we know all the sides are <math>13</math> and the angles are mostly complementary). Thus, we create a [[square]] with sides <math>5 + 12 = 17</math>. | ||
| Line 10: | Line 14: | ||
<math>\overline{EF}</math> is the diagonal of the square, with length <math>17\sqrt{2}</math>; the answer is <math>EF^2 = (17\sqrt{2})^2 = 578</math>. | <math>\overline{EF}</math> is the diagonal of the square, with length <math>17\sqrt{2}</math>; the answer is <math>EF^2 = (17\sqrt{2})^2 = 578</math>. | ||
| + | |||
| + | |||
| + | == '''Solution 2.''' == | ||
| + | |||
| + | |||
| + | A slightly more analytic/brute-force approach: | ||
| + | |||
| + | Drop perpendiculars from <math>E</math> and <math>F</math> to <math>I</math> and <math>J</math>, respectively; construct right triangle <math>EKF</math> with right angle at K and <math>EK || BC</math>. Since <math>2[CDF]=DF*CF=CD*JF</math>, we have <math>JF=5\times12/13 = \frac{60}{13}</math>. Similarly, <math>EI=\frac{60}{13}</math>. Since <math>\triangle DJF \sim \triangle DFC</math>, we have <math>DJ=\frac{5JF}{12}=\frac{25}{13}</math>. | ||
| + | |||
| + | Now, we see that <math>FK=DC-(DJ+IB)=DC-2DJ=13-\frac{50}{13}=\frac{119}{13}</math>. Also, <math>EK=BC+(JF+IE)=BC+2JF=13+\frac{120}{13}=\frac{289}{13}</math>. By the Pythagorean Theorem, we have <math>EF=\sqrt{\left(\frac{289}{13}\right)^2+\left(\frac{119}{13} \right)^2}=\frac{\sqrt{(17^2)(17^2+7^2)}}{13}=\frac{17\sqrt{338}}{13}=\frac{17(13\sqrt{2})}{13}=17\sqrt{2}</math>. Therefore, <math>EF^2=(17\sqrt{2})^2=578</math>. | ||
== See also == | == See also == | ||
Revision as of 19:27, 31 March 2007
Problem
Square ![]() has side length
has side length ![]() , and points
, and points ![]() and
and ![]() are exterior to the square such that
are exterior to the square such that ![]() and
and ![]() . Find
. Find ![]() .
.
Solution
Solution 1.
Extend ![]() and
and ![]() to their points of intersection. Since
to their points of intersection. Since ![]() and are both
and are both ![]() right triangles, we can come to the conclusion that the two new triangles are also congruent to these two (use ASA, as we know all the sides are
right triangles, we can come to the conclusion that the two new triangles are also congruent to these two (use ASA, as we know all the sides are ![]() and the angles are mostly complementary). Thus, we create a square with sides
and the angles are mostly complementary). Thus, we create a square with sides ![]() .
.
![]() is the diagonal of the square, with length
is the diagonal of the square, with length ![]() ; the answer is
; the answer is ![]() .
.
Solution 2.
A slightly more analytic/brute-force approach:
Drop perpendiculars from ![]() and
and ![]() to
to ![]() and
and ![]() , respectively; construct right triangle
, respectively; construct right triangle ![]() with right angle at K and
with right angle at K and ![]() . Since
. Since ![]() , we have
, we have ![]() . Similarly,
. Similarly, ![]() . Since
. Since ![]() , we have
, we have ![]() .
.
Now, we see that ![]() . Also,
. Also, ![]() . By the Pythagorean Theorem, we have
. By the Pythagorean Theorem, we have  . Therefore,
. Therefore, ![]() .
.
See also
| 2007 AIME II (Problems • Answer Key • Resources) | ||
| Preceded by Problem 2 |
Followed by Problem 4 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||