2007 AMC 10B Problems/Problem 21
Contents
Problem
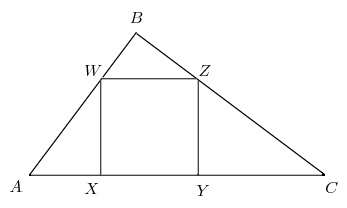
Right ![]() has
has ![]() and
and ![]() Square
Square ![]() is inscribed in
is inscribed in ![]() with
with ![]() and
and ![]() on
on ![]() on
on ![]() and
and ![]() on
on ![]() What is the side length of the square?
What is the side length of the square?
![]()
Solution 1
There are many similar triangles in the diagram, but we will only use ![]() If
If ![]() is the altitude from
is the altitude from ![]() to
to ![]() and
and ![]() is the sidelength of the square, then
is the sidelength of the square, then ![]() is the altitude from
is the altitude from ![]() to
to ![]() By similar triangles,
By similar triangles,

Find the length of the altitude of ![]() Since it is a right triangle, the area of
Since it is a right triangle, the area of ![]() is
is ![]()
The area can also be expressed as ![]() so
so ![]()
Substitute back into ![]()
![]()
Solution 2
Let ![]() be the side length of the inscribed square. Note that
be the side length of the inscribed square. Note that ![]() .
.
Then we can setup the following ratios:
![]()
![]()
But then ![]()
See Also
| 2007 AMC 10B (Problems • Answer Key • Resources) | ||
| Preceded by Problem 20 |
Followed by Problem 22 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.