Difference between revisions of "2007 AMC 12A Problems/Problem 19"
(→Problem) |
(→Problem) |
||
| Line 1: | Line 1: | ||
== Problem == | == Problem == | ||
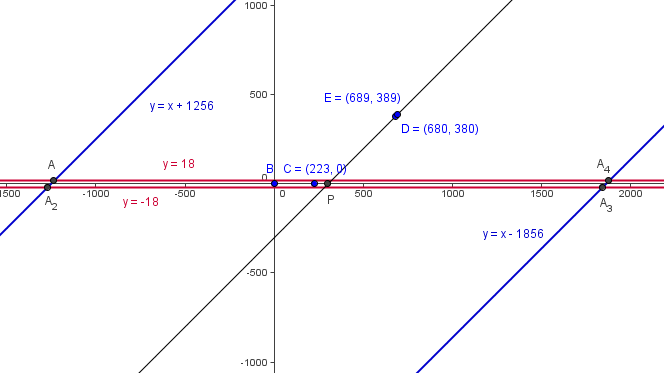
| − | [[Triangle]]s <math>ABC</math> and <math>ADE</math> have [[area]]s <math>2007</math> and <math>7002,</math> respectively, with <math>B = (0,0),</math> <math>C = (223,0),</math> <math>D = (680,380),</math> and <math>E = (689,389).</math> What is the sum of all possible x | + | [[Triangle]]s <math>ABC</math> and <math>ADE</math> have [[area]]s <math>2007</math> and <math>7002,</math> respectively, with <math>B = (0,0),</math> <math>C = (223,0),</math> <math>D = (680,380),</math> and <math>E = (689,389).</math> What is the sum of all possible x coordinates of <math>A</math>? |
<math>\mathrm{(A)}\ 282 \qquad \mathrm{(B)}\ 300 \qquad \mathrm{(C)}\ 600 \qquad \mathrm{(D)}\ 900 \qquad \mathrm{(E)}\ 1200</math> | <math>\mathrm{(A)}\ 282 \qquad \mathrm{(B)}\ 300 \qquad \mathrm{(C)}\ 600 \qquad \mathrm{(D)}\ 900 \qquad \mathrm{(E)}\ 1200</math> | ||
Revision as of 11:21, 14 October 2018
Problem
Triangles ![]() and
and ![]() have areas
have areas ![]() and
and ![]() respectively, with
respectively, with ![]()
![]()
![]() and
and ![]() What is the sum of all possible x coordinates of
What is the sum of all possible x coordinates of ![]() ?
?
![]()
Solution
Solution 1
From ![]() , we have that the height of
, we have that the height of ![]() is
is ![]() . Thus
. Thus ![]() lies on the lines
lies on the lines ![]() .
.
![]() using 45-45-90 triangles, so in
using 45-45-90 triangles, so in ![]() we have that
we have that ![]() . The slope of
. The slope of ![]() is
is ![]() , so the equation of the line is
, so the equation of the line is ![]() . The point
. The point ![]() lies on one of two parallel lines that are
lies on one of two parallel lines that are ![]() units away from
units away from ![]() . Now take an arbitrary point on the line
. Now take an arbitrary point on the line ![]() and draw the perpendicular to one of the parallel lines; then draw a line straight down from the same arbitrary point. These form a 45-45-90
and draw the perpendicular to one of the parallel lines; then draw a line straight down from the same arbitrary point. These form a 45-45-90 ![]() , so the straight line down has a length of
, so the straight line down has a length of ![]() . Now we note that the y-intercept of the parallel lines is either
. Now we note that the y-intercept of the parallel lines is either ![]() units above or below the y-intercept of line
units above or below the y-intercept of line ![]() ; hence the equation of the parallel lines is
; hence the equation of the parallel lines is ![]() .
.
We just need to find the intersections of these two lines and sum up the values of the x-coordinates. Substituting the ![]() into
into ![]() , we get
, we get ![]() .
.
Solution 2
We are finding the intersection of two pairs of parallel lines, which will form a parallelogram. The centroid of this parallelogram is just the intersection of ![]() and
and ![]() , which can easily be calculated to be
, which can easily be calculated to be ![]() . Now the sum of the x-coordinates is just
. Now the sum of the x-coordinates is just ![]() .
.
See also
| 2007 AMC 12A (Problems • Answer Key • Resources) | |
| Preceded by Problem 18 |
Followed by Problem 20 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.