Difference between revisions of "2007 AMC 8 Problems/Problem 11"
(Created page with '== Problem == Tiles <math>I, II, III</math> and <math>IV</math> are translated so one tile coincides with each of the rectangles <math>A, B, C</math> and <math>D</math>. In the …') |
Basketball8 (talk | contribs) (→Solution) |
||
| Line 14: | Line 14: | ||
<center>[[Image:AMC8_2007_11S.png]]</center> | <center>[[Image:AMC8_2007_11S.png]]</center> | ||
| + | |||
| + | ==See Also== | ||
| + | {{AMC8 box|year=2007|num-b=10|num-a=12}} | ||
Revision as of 23:37, 12 November 2012
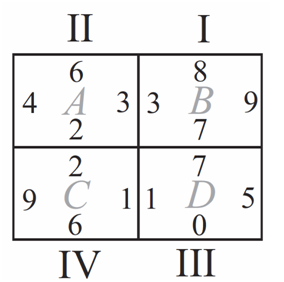
Problem
Tiles ![]() and
and ![]() are translated so one tile coincides with each of the rectangles
are translated so one tile coincides with each of the rectangles ![]() and
and ![]() . In the final arrangement, the two numbers on any side common to two adjacent tiles must be the same. Which of the tiles is translated to Rectangle
. In the final arrangement, the two numbers on any side common to two adjacent tiles must be the same. Which of the tiles is translated to Rectangle ![]() ?
?

![]() cannot be determined
cannot be determined
Solution
We first notice that tile III has a ![]() on the bottom and a
on the bottom and a ![]() on the right side. Since no other tile has a
on the right side. Since no other tile has a ![]() or a
or a ![]() , Tile III must be in rectangle
, Tile III must be in rectangle ![]() . Tile III also has a
. Tile III also has a ![]() on the left, so Tile IV must be in Rectangle
on the left, so Tile IV must be in Rectangle ![]() .
.
The answer is ![]()
See Also
| 2007 AMC 8 (Problems • Answer Key • Resources) | ||
| Preceded by Problem 10 |
Followed by Problem 12 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AJHSME/AMC 8 Problems and Solutions | ||









