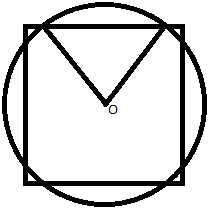
2010 AMC 10B Problems/Problem 16
The radius of circle is ![]()
Half the diagonal of the square is ![]() . We can see that the circle passes outside the square, but the square is NOT completely contained in the circle
. We can see that the circle passes outside the square, but the square is NOT completely contained in the circle
Therefore the picture will look something like this:
Then we proceed to find: 4 * (area of the sector marked off by the two radii drawn - area of the triangle with side on the square and the two radii).
To find this, we do the following:
First we realize that the radius perpendicular to the side of the square between the extra lines marking off the sector splits the chord in half. Let this half-length be ![]() . Power of a point states that if two chords (AB and CD) intersect at X, then AX
. Power of a point states that if two chords (AB and CD) intersect at X, then AX![]() BX
BX![]() CX
CX![]() DX. Applying power of a point to this situation,
DX. Applying power of a point to this situation, ![]() . (We know the center of a square to be halfway in each direction, if you know what I mean by direction).
. (We know the center of a square to be halfway in each direction, if you know what I mean by direction).
Solving, ![]() . The significance? This means the chord is equal to the radius of a circle, so the sector has angle
. The significance? This means the chord is equal to the radius of a circle, so the sector has angle ![]() . Since this is a sixth of the circle, the sector has area
. Since this is a sixth of the circle, the sector has area ![]() .
.
Now we turn to the triangle.
Since it is equilateral, we know it has area equal to ![]() times the square of its sidelength. Therefore, our triangle has area
times the square of its sidelength. Therefore, our triangle has area ![]() .
.
Putting it together, we get the answer to be $4\left( \frac{\pi}{18}-\frac{\sqrt{3}{12} \right)=$ (Error compiling LaTeX. Unknown error_msg)
![]()