Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

2010 AMC 12A Problems/Problem 8

Revision as of 16:39, 10 March 2020 by Vsamc (talk | contribs)

Problem

Triangle $ABC$ has $AB=2 \cdot AC$. Let $D$ and $E$ be on $\overline{AB}$ and $\overline{BC}$, respectively, such that $\angle BAE = \angle ACD$. Let $F$ be the intersection of segments $AE$ and $CD$, and suppose that $\triangle CFE$ is equilateral. What is $\angle ACB$?

$\textbf{(A)}\ 60^\circ \qquad \textbf{(B)}\ 75^\circ \qquad \textbf{(C)}\ 90^\circ \qquad \textbf{(D)}\ 105^\circ \qquad \textbf{(E)}\ 120^\circ$

Solution

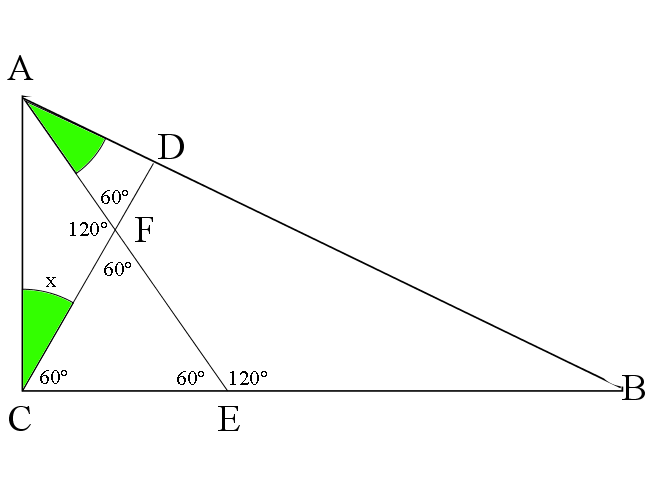
AMC 2010 12A Problem 8.png


Let $\angle BAE = \angle ACD = x$.

\begin{align*}\angle BCD &= \angle AEC = 60^\circ\\ \angle EAC + \angle FCA + \angle ECF + \angle AEC &= \angle EAC + x + 60^\circ + 60^\circ = 180^\circ\\ \angle EAC &= 60^\circ - x\\ \angle BAC &= \angle EAC + \angle BAE = 60^\circ - x + x = 60^\circ\end{align*}

Since $\frac{AC}{AB} = \frac{1}{2}$, triangle $ABC$ is a $30-60-90$ triangle, so $\angle BCA = \boxed{90^\circ\,\textbf{(C)}}$.

Solution 2(Trig and Angle Chasing)

Let $AB=2a, AC=a$. Let $\angle BAE=\angle ACD=x$. Because $\triangle CFE$ is equilateral, we get $\angle FCE=60$, so $\angle ACB=60+x$. Because $\triangle CFE$ is equilateral, we get $\angle CFE=60$. Angles $AFD$ and $CFE$ are vertical, so $\angle AFD=60$. By triangle $ADF$, we have $\angle ADF=120-x$, and because of line $AB$, we have $\angle BDC=60+x$. Because Of line $BC$, we have $\angle AEB=120$, and by line $CD$, we have $\angle DFE=120$. By quadrilateral $BDFE$, we have $\angle ABC=60-x$.

By the Law of Sines, we have $\frac{\sin(60-x)}{a}=\frac{\sin(60+x)}{2a}\implies$\sin(60-x)=\frac{\sin(60+x)}{2}\implies 2\sin(60-x)=\sin(60+x)$. By the sine addition formula(which states$\sin(a+b)=\sin(a)\cos(b)+\cos(a)\sin(b)$by the way), we have$2(\sin(60)\cos(-x)+\cos(60)\sin(-x))=\sin(60)\cos(x)+\cos(60)\sin(x)$. Because cosine is an even function, and sine is an odd function, we have$2\sin(60)\cos(x)-2\cos(60)\sin(x)=\sin(60)\cos(x)+\cos(60)\sin(x) \implies \sin(60)\cos(x)=3\cos(60)\sin(x)$. We know that$\sin(60)=\frac{\sqrt{3}}{2}$, and$\cos(60)=\frac{1}{2}$, hence$\frac{\sqrt{3}}{2}\cos(x)=\frac{3}{2}\sin(x)\implies $\tan(x)=\frac{\sqrt(3)}{3}$. The only value of $x$ that satisfies $60+x<180$(because $60+x$ is an angle of the triangle)$is$x=30^{\circ}$. We seek to find$\angle ACB$, which as we found before is$60+x$, which is$90$. The answer is (C)

-vsamc

See also

2010 AMC 12A (Problems • Answer Key • Resources)
Preceded by
Problem 7 		Followed by
Problem 9
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2010_AMC_12A_Problems/Problem_8&oldid=119011"