Difference between revisions of "2011 AIME II Problems/Problem 10"
(Created page with 'Problem: A circle with center O has radius 25. Chord <math>\overline{AB}</math> of length 30 and chord <math>\overline{CD}</math> of length 14 intersect at point P. The distance…') |
Treehead123 (talk | contribs) m (→Solution 7 Analytic Geometry) |
||
| (36 intermediate revisions by 23 users not shown) | |||
| Line 1: | Line 1: | ||
| − | Problem | + | == Problem 10 == |
| + | A [[circle]] with center <math>O</math> has radius 25. [[Chord]] <math>\overline{AB}</math> of length 30 and chord <math>\overline{CD}</math> of length 14 intersect at point <math>P</math>. The distance between the [[midpoint]]s of the two chords is 12. The quantity <math>OP^2</math> can be represented as <math>\frac{m}{n}</math>, where <math>m</math> and <math>n</math> are [[relatively prime]] positive integers. Find the remainder when <math>m + n</math> is divided by 1000. | ||
| − | + | == Solution 1 == | |
| + | Let <math>E</math> and <math>F</math> be the midpoints of <math>\overline{AB}</math> and <math>\overline{CD}</math>, respectively, such that <math>\overline{BE}</math> intersects <math>\overline{CF}</math>. | ||
| + | |||
| + | Since <math>E</math> and <math>F</math> are midpoints, <math>BE = 15</math> and <math>CF = 7</math>. | ||
| + | |||
| + | <math>B</math> and <math>C</math> are located on the circumference of the circle, so <math>OB = OC = 25</math>. | ||
| + | |||
| + | The line through the midpoint of a chord of a circle and the center of that circle is perpendicular to that chord, so <math>\triangle OEB</math> and <math>\triangle OFC</math> are right triangles (with <math>\angle OEB</math> and <math>\angle OFC</math> being the right angles). By the Pythagorean Theorem, <math>OE = \sqrt{25^2 - 15^2} = 20</math>, and <math>OF = \sqrt{25^2 - 7^2} = 24</math>. | ||
| + | |||
| + | Let <math>x</math>, <math>a</math>, and <math>b</math> be lengths <math>OP</math>, <math>EP</math>, and <math>FP</math>, respectively. OEP and OFP are also right triangles, so <math>x^2 = a^2 + 20^2 \to a^2 = x^2 - 400</math>, and <math>x^2 = b^2 + 24^2 \to b^2 = x^2 - 576</math> | ||
| + | |||
| + | We are given that <math>EF</math> has length 12, so, using the [[Law of Cosines]] with <math>\triangle EPF</math>: | ||
| + | |||
| + | <math>12^2 = a^2 + b^2 - 2ab \cos (\angle EPF) = a^2 + b^2 - 2ab \cos (\angle EPO + \angle FPO)</math> | ||
| + | |||
| + | Substituting for <math>a</math> and <math>b</math>, and applying the Cosine of Sum formula: | ||
| + | |||
| + | <math>144 = (x^2 - 400) + (x^2 - 576) - 2 \sqrt{x^2 - 400} \sqrt{x^2 - 576} \left( \cos \angle EPO \cos \angle FPO - \sin \angle EPO \sin \angle FPO \right)</math> | ||
| + | |||
| + | <math>\angle EPO</math> and <math>\angle FPO</math> are acute angles in right triangles, so substitute opposite/hypotenuse for sines and adjacent/hypotenuse for cosines: | ||
| + | |||
| + | <math>144 = 2x^2 - 976 - 2 \sqrt{(x^2 - 400)(x^2 - 576)} \left(\frac{\sqrt{x^2 - 400}}{x} \frac{\sqrt{x^2 - 576}}{x} - \frac{20}{x} \frac{24}{x} \right)</math> | ||
| + | |||
| + | Combine terms and multiply both sides by <math>x^2</math>: <math>144 x^2 = 2 x^4 - 976 x^2 - 2 (x^2 - 400) (x^2 - 576) + 960 \sqrt{(x^2 - 400)(x^2 - 576)}</math> | ||
| + | |||
| + | Combine terms again, and divide both sides by 64: <math>13 x^2 = 7200 - 15 \sqrt{x^4 - 976 x^2 + 230400}</math> | ||
| + | |||
| + | Square both sides: <math>169 x^4 - 187000 x^2 + 51,840,000 = 225 x^4 - 219600 x^2 + 51,840,000</math> | ||
| + | |||
| + | This reduces to <math>x^2 = \frac{4050}{7} = (OP)^2</math>; <math>4050 + 7 \equiv \boxed{057} \pmod{1000}</math>. | ||
| + | |||
| + | ==Solution 2 - Fastest== | ||
| + | |||
| + | We begin as in the first solution. Once we see that <math>\triangle EOF</math> has side lengths <math>12</math>, <math>20</math>, and <math>24</math>, we can compute its area with Heron's formula: | ||
| + | |||
| + | <cmath>K = \sqrt{s(s-a)(s-b)(s-c)} = \sqrt{28\cdot 16\cdot 8\cdot 4} = 32\sqrt{14}.</cmath> | ||
| + | |||
| + | Thus, the circumradius of triangle <math>\triangle EOF</math> is <math>R = \frac{abc}{4K} = \frac{45}{\sqrt{14}}</math>. Looking at <math>EPFO</math>, we see that <math>\angle OEP = \angle OFP = 90^\circ</math>, which makes it a cyclic quadrilateral. This means <math>\triangle EOF</math>'s circumcircle and <math>EPFO</math>'s inscribed circle are the same. | ||
| + | |||
| + | Since <math>EPFO</math> is [[cyclic]] with diameter <math>OP</math>, we have <math>OP = 2R = \frac{90}{\sqrt{14}}</math>, so <math>OP^2 = \frac{4050}{7}</math> and the answer is <math>\boxed{057}</math>. | ||
| + | |||
| + | ==Solution 3== | ||
| + | |||
| + | We begin as the first solution have <math>OE=20</math> and <math>OF=24</math>. Because <math>\angle PEF+\angle PFO=180^{\circ}</math>, Quadrilateral <math>EPFO</math> is inscribed in a Circle. Assume point <math>I</math> is the center of this circle. | ||
| + | |||
| + | <math>\because \angle OEP=90^{\circ}</math> | ||
| + | |||
| + | <math>\therefore</math> point <math>I</math> is on <math>OP</math> | ||
| + | |||
| + | Link <math>EI</math> and <math>FI</math>, Made line <math>IK\bot EF</math>, then <math>\angle EIK=\angle EOF</math> | ||
| + | |||
| + | On the other hand, <math>\cos\angle EOF=\frac{EO^2+OF^2-EF^2}{2\cdot EO\cdot OF}=\frac{13}{15}=\cos\angle EIK</math> | ||
| + | |||
| + | <math>\sin\angle EOF=\sin\angle EIK=\sqrt{1-\frac{13^2}{15^2}}=\frac{2\sqrt{14}}{15}</math> | ||
| + | |||
| + | As a result, <math>IE=IO=\frac{45}{\sqrt 14}</math> | ||
| + | |||
| + | Therefore, <math>OP^2=4\cdot \frac{45^2}{14}=\frac{4050}{7}.</math> | ||
| + | |||
| + | As a result, <math>m+n=4057\equiv \boxed{057}\pmod{1000}</math> | ||
| + | |||
| + | ==Solution 4== | ||
| + | |||
| + | Let <math>OP=x</math>. | ||
| + | |||
| + | Proceed as the first solution in finding that quadrilateral <math>EPFO</math> has side lengths <math>OE=20</math>, <math>OF=24</math>, <math>EP=\sqrt{x^2-20^2}</math>, and <math>PF=\sqrt{x^2-24^2}</math>, and diagonals <math>OP=x</math> and <math>EF=12</math>. | ||
| + | |||
| + | We note that quadrilateral <math>EPFO</math> is cyclic and use Ptolemy's theorem to solve for <math>x</math>: | ||
| + | |||
| + | <cmath>20\cdot \sqrt{x^2-24^2} + 12\cdot x = 24\cdot \sqrt{x^2-20^2}</cmath> | ||
| + | |||
| + | Solving, we have <math>x^2=\frac{4050}{7}</math> so the answer is <math>\boxed{057}</math>. | ||
| + | |||
| + | -Solution by blueberrieejam | ||
| + | |||
| + | ~bluesoul changes the equation to a right equation, the previous equation isn't solvable | ||
| + | |||
| + | ==Solution 5 (Quick Angle Solution)== | ||
| + | Let <math>M</math> be the midpoint of <math>AB</math> and <math>N</math> of <math>CD</math>. As <math>\angle OMP = \angle ONP</math>, quadrilateral <math>OMPN</math> is cyclic with diameter <math>OP</math>. By Cyclic quadrilaterals note that <math>\angle MPO = \angle MNO</math>. | ||
| + | |||
| + | The area of <math>\triangle MNP</math> can be computed by Herons as <cmath>[MNO] = \sqrt{s(s-a)(s-b)(s-c)} = \sqrt{28\cdot 16\cdot 8\cdot 4} = 32\sqrt{14}.</cmath> The area is also <math>\frac{1}{2}ON \cdot MN \sin{\angle MNO}</math>. Therefore, | ||
| + | <cmath>\begin{align*} | ||
| + | \sin{\angle MNO} &= \frac{2[MNO]}{ON \cdot MN} \\ | ||
| + | &= \frac{2}{9}\sqrt{14} \\ | ||
| + | \sin{\angle MNO} &= \frac{OM}{OP} \\ | ||
| + | &= \frac{2}{9}\sqrt{14} \\ | ||
| + | OP &= \frac{90\sqrt{14}}{14} \\ | ||
| + | OP^2 &= \frac{4050}{7} \implies \boxed{057}. | ||
| + | \end{align*}</cmath> | ||
| + | |||
| + | ~ Aaryabhatta1 | ||
| + | |||
| + | ==Solution 6== | ||
| + | Define <math>M</math> and <math>N</math> as the midpoints of <math>AB</math> and <math>CD</math>, respectively. Because <math>\angle OMP = \angle ONP = 90^{\circ}</math>, we have that <math>ONPM</math> is a cyclic quadrilateral. Hence, <math>\angle PNM = \angle POM.</math> Then, let these two angles be denoted as <math>\alpha</math>. | ||
| + | Now, assume WLOG that <math>PD = x < 7</math> and <math>PB = y < 15</math> (We can do this because one of <math>PD</math> or <math>PC</math> must be less than 7, and similarly for <math>PB</math> and <math>PA</math>). Then, by Power of a Point on P with respect to the circle with center <math>O</math>, we have that | ||
| + | <cmath>(14-x)x = (30-y)y</cmath> | ||
| + | <cmath>(7-x)^{2}+176=(15-y)^{2}.</cmath> | ||
| + | Then, let <math>z = (7-x)^{2}</math>. From Law of Cosines on <math>\triangle NMP</math>, we have that | ||
| + | <cmath>\textrm{cos } \angle MNP = \frac{NP^{2}+MN^{2}-MP^{2}}{2 \cdot NP \cdot MN} </cmath> | ||
| + | <cmath>\textrm{cos } \alpha = \frac{(7-x)^{2} + 12^{2} - (14-x)^{2}}{24 \cdot (7-x)}.</cmath> | ||
| + | Plugging in <math>z</math> in gives | ||
| + | <cmath>\textrm{cos } \alpha = \frac{-32}{24 \cdot \sqrt{z}}</cmath> | ||
| + | <cmath>\textrm{cos } \alpha = \frac{-4}{3\sqrt{z}}</cmath> | ||
| + | <cmath>\textrm{cos }^{2} \alpha = \frac{16}{9z}.</cmath> | ||
| + | Hence, | ||
| + | <cmath>\textrm{tan }^{2} \alpha = \frac{\frac{9z-16}{9z}}{\frac{16}{9z}} = \frac{9z-16}{16}.</cmath> | ||
| + | Then, we also know that | ||
| + | <cmath>\textrm{tan } \alpha = \textrm{tan } \angle MOP = \frac{MP}{OM} = \frac{14-y}{20}.</cmath> | ||
| + | Squaring this, we get | ||
| + | <cmath>\textrm{tan }^{2} \alpha = \frac{z+176}{400}.</cmath> | ||
| + | Equating our expressions for <math>z</math>, we get | ||
| + | <math>\frac{z+176}{400} = \frac{9z-16}{16}.</math> | ||
| + | Solving gives us that | ||
| + | <math>z = \frac{18}{7}</math>. | ||
| + | Since <math>\angle ONP = 90^{\circ}</math>, from the Pythagorean Theorem, | ||
| + | <math>OP^{2} = ON^{2}+PN^{2} = 25^{2}-7^{2} + z = 576+z = \frac{4050}{7}</math>, | ||
| + | and thus the answer is <math>4050+7 = 4057</math>, which when divided by a thousand leaves a remainder of <math>\boxed{57}.</math> | ||
| + | |||
| + | -Mr.Sharkman | ||
| + | |||
| + | Note: my solution was very long and tedious. It was definitely was the least elegant solution. The only thing I like about it is it contains no quadratic equations (unless you count LoC). | ||
| + | |||
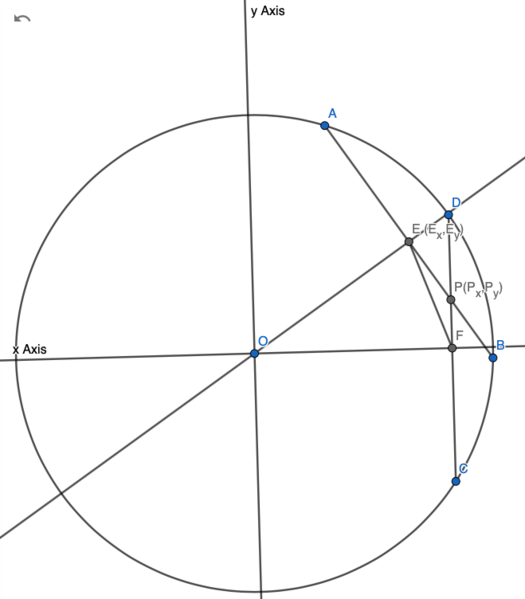
| + | ==Solution 7 Analytic Geometry== | ||
| + | [[Image:2011 AIMEII Problem 10 CASE 2.png|525px]] | ||
| + | |||
| + | Let <math>E</math> and <math>F</math> be the midpoints of <math>\overline{AB}</math> and <math>\overline{CD}</math>, respectively, such that <math>\overline{BE}</math> intersects <math>\overline{CF}</math>. | ||
| + | |||
| + | Since <math>E</math> and <math>F</math> are midpoints, <math>BE = 15</math> and <math>CF = 7</math>. | ||
| + | |||
| + | <math>B</math> and <math>C</math> are located on the circumference of the circle, so <math>OB = OC = 25</math>. | ||
| + | |||
| + | Since <math>\overline{OE}\perp \overline{AB}</math> and <math>\overline{OF}\perp \overline{CD}</math>, | ||
| + | <math>OE = \sqrt{OB^2-BE^2}=20</math> and <math>OF = \sqrt{OC^2-OF^2}=24</math> | ||
| + | |||
| + | With law of cosines, <math>\cos \angle EOF = \frac{OE^2+OF^2-EF^2}{2\cdot OE\cdot OF} = \frac{13}{15}</math> | ||
| + | |||
| + | Since <math>EF < OF</math>, <math>\angle EOF</math> is acute angle. <math>\sin \angle EOF = \sqrt{1-\cos^2 \angle EOF} = \frac{\sqrt{56}}{15}</math> and <math>\tan \angle EOF = \frac{\sqrt{56}}{13}</math> | ||
| + | |||
| + | Let <math>\overline{OF}</math> line be <math>x</math> axis. | ||
| + | |||
| + | Line <math>\overline{DC}</math> equation is <math>x = OF</math>. | ||
| + | |||
| + | Since line <math>\overline{AB}</math> passes point <math>E</math> and perpendicular to <math>\overline{OD}</math>, its equation is <math>y - E_y = -\frac{1}{\tan \angle EOF} (x - E_x)</math> | ||
| + | |||
| + | where <math>E_x = OE\cos{\angle EOF}</math> , <math>E_y = OE\sin{\angle EOF}</math> | ||
| + | |||
| + | Since <math>P</math> is the intersection of <math>\overline{AB}</math> and <math>\overline{CD}</math>, | ||
| + | |||
| + | <math>P_x = OF = 24</math> | ||
| + | |||
| + | <math>P_y = E_y -\frac{1}{\tan \angle EOF} (OF - E_x) = - \frac{3\sqrt{14}}{7}</math> (Negative means point <math>P</math> is between point <math>F</math> and <math>C</math>) | ||
| + | |||
| + | <math>OP^2 = P_x^2 + P_y^2 = \frac{4050}{7}</math> and the answer is <math>\boxed{057}</math>. | ||
| + | |||
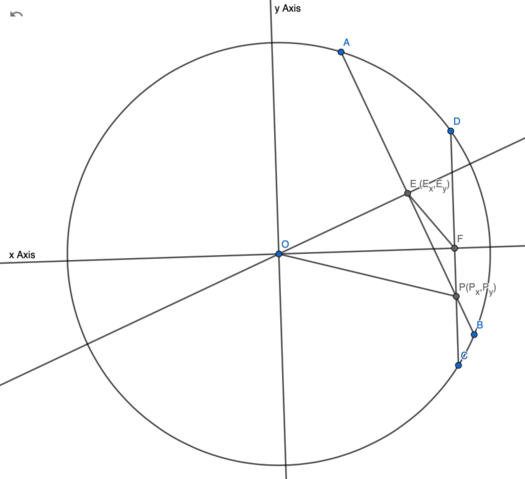
| + | Note: if <math>EF</math> was longer, point <math>P</math> would be between point <math>D</math> and <math>F</math>. Then, <math>OP</math> would be the diagonal of quadrilateral <math>OEPF</math> not the side. To apply Ptolemy's theorem like solution 4, it is critical to know whether <math>OP</math> is the diagonal or side of quadrilateral. Equation for wrong case cannot be solved. For example, | ||
| + | |||
| + | [[Image:2011 AIMEII Problem 10 CASE 1.png|525px]] | ||
| + | |||
| + | ==See also== | ||
| + | {{AIME box|year=2011|n=II|num-b=9|num-a=11}} | ||
| + | |||
| + | [[Category:Intermediate Geometry Problems]] | ||
| + | {{MAA Notice}} | ||
Latest revision as of 03:12, 18 December 2023
Contents
Problem 10
A circle with center ![]() has radius 25. Chord
has radius 25. Chord ![]() of length 30 and chord
of length 30 and chord ![]() of length 14 intersect at point
of length 14 intersect at point ![]() . The distance between the midpoints of the two chords is 12. The quantity
. The distance between the midpoints of the two chords is 12. The quantity ![]() can be represented as
can be represented as ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers. Find the remainder when
are relatively prime positive integers. Find the remainder when ![]() is divided by 1000.
is divided by 1000.
Solution 1
Let ![]() and
and ![]() be the midpoints of
be the midpoints of ![]() and
and ![]() , respectively, such that
, respectively, such that ![]() intersects
intersects ![]() .
.
Since ![]() and
and ![]() are midpoints,
are midpoints, ![]() and
and ![]() .
.
![]() and
and ![]() are located on the circumference of the circle, so
are located on the circumference of the circle, so ![]() .
.
The line through the midpoint of a chord of a circle and the center of that circle is perpendicular to that chord, so ![]() and
and ![]() are right triangles (with
are right triangles (with ![]() and
and ![]() being the right angles). By the Pythagorean Theorem,
being the right angles). By the Pythagorean Theorem, ![]() , and
, and ![]() .
.
Let ![]() ,
, ![]() , and
, and ![]() be lengths
be lengths ![]() ,
, ![]() , and
, and ![]() , respectively. OEP and OFP are also right triangles, so
, respectively. OEP and OFP are also right triangles, so ![]() , and
, and ![]()
We are given that ![]() has length 12, so, using the Law of Cosines with
has length 12, so, using the Law of Cosines with ![]() :
:
![]()
Substituting for ![]() and
and ![]() , and applying the Cosine of Sum formula:
, and applying the Cosine of Sum formula:
![]()
![]() and
and ![]() are acute angles in right triangles, so substitute opposite/hypotenuse for sines and adjacent/hypotenuse for cosines:
are acute angles in right triangles, so substitute opposite/hypotenuse for sines and adjacent/hypotenuse for cosines:

Combine terms and multiply both sides by ![]() :
: ![]()
Combine terms again, and divide both sides by 64: ![]()
Square both sides: ![]()
This reduces to ![]() ;
; ![]() .
.
Solution 2 - Fastest
We begin as in the first solution. Once we see that ![]() has side lengths
has side lengths ![]() ,
, ![]() , and
, and ![]() , we can compute its area with Heron's formula:
, we can compute its area with Heron's formula:
![]()
Thus, the circumradius of triangle ![]() is
is ![]() . Looking at
. Looking at ![]() , we see that
, we see that ![]() , which makes it a cyclic quadrilateral. This means
, which makes it a cyclic quadrilateral. This means ![]() 's circumcircle and
's circumcircle and ![]() 's inscribed circle are the same.
's inscribed circle are the same.
Since ![]() is cyclic with diameter
is cyclic with diameter ![]() , we have
, we have ![]() , so
, so ![]() and the answer is
and the answer is ![]() .
.
Solution 3
We begin as the first solution have ![]() and
and ![]() . Because
. Because ![]() , Quadrilateral
, Quadrilateral ![]() is inscribed in a Circle. Assume point
is inscribed in a Circle. Assume point ![]() is the center of this circle.
is the center of this circle.
![]()
![]() point
point ![]() is on
is on ![]()
Link ![]() and
and ![]() , Made line
, Made line ![]() , then
, then ![]()
On the other hand, ![]()
![]()
As a result, ![]()
Therefore, ![]()
As a result, ![]()
Solution 4
Let ![]() .
.
Proceed as the first solution in finding that quadrilateral ![]() has side lengths
has side lengths ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , and diagonals
, and diagonals ![]() and
and ![]() .
.
We note that quadrilateral ![]() is cyclic and use Ptolemy's theorem to solve for
is cyclic and use Ptolemy's theorem to solve for ![]() :
:
![]()
Solving, we have ![]() so the answer is
so the answer is ![]() .
.
-Solution by blueberrieejam
~bluesoul changes the equation to a right equation, the previous equation isn't solvable
Solution 5 (Quick Angle Solution)
Let ![]() be the midpoint of
be the midpoint of ![]() and
and ![]() of
of ![]() . As
. As ![]() , quadrilateral
, quadrilateral ![]() is cyclic with diameter
is cyclic with diameter ![]() . By Cyclic quadrilaterals note that
. By Cyclic quadrilaterals note that ![]() .
.
The area of ![]() can be computed by Herons as
can be computed by Herons as ![]() The area is also
The area is also ![]() . Therefore,
. Therefore,
![\begin{align*} \sin{\angle MNO} &= \frac{2[MNO]}{ON \cdot MN} \\ &= \frac{2}{9}\sqrt{14} \\ \sin{\angle MNO} &= \frac{OM}{OP} \\ &= \frac{2}{9}\sqrt{14} \\ OP &= \frac{90\sqrt{14}}{14} \\ OP^2 &= \frac{4050}{7} \implies \boxed{057}. \end{align*}](http://latex.artofproblemsolving.com/c/9/a/c9ac27140d40c3ee394c8efb3e156e2c36a45941.png)
~ Aaryabhatta1
Solution 6
Define ![]() and
and ![]() as the midpoints of
as the midpoints of ![]() and
and ![]() , respectively. Because
, respectively. Because ![]() , we have that
, we have that ![]() is a cyclic quadrilateral. Hence,
is a cyclic quadrilateral. Hence, ![]() Then, let these two angles be denoted as
Then, let these two angles be denoted as ![]() .
Now, assume WLOG that
.
Now, assume WLOG that ![]() and
and ![]() (We can do this because one of
(We can do this because one of ![]() or
or ![]() must be less than 7, and similarly for
must be less than 7, and similarly for ![]() and
and ![]() ). Then, by Power of a Point on P with respect to the circle with center
). Then, by Power of a Point on P with respect to the circle with center ![]() , we have that
, we have that
![]()
![]() Then, let
Then, let ![]() . From Law of Cosines on
. From Law of Cosines on ![]() , we have that
, we have that
![]()
![]() Plugging in
Plugging in ![]() in gives
in gives
![]()
![]()
![]() Hence,
Hence,
![]() Then, we also know that
Then, we also know that
![]() Squaring this, we get
Squaring this, we get
![]() Equating our expressions for
Equating our expressions for ![]() , we get
, we get
![]() Solving gives us that
Solving gives us that
![]() .
Since
.
Since ![]() , from the Pythagorean Theorem,
, from the Pythagorean Theorem,
![]() ,
and thus the answer is
,
and thus the answer is ![]() , which when divided by a thousand leaves a remainder of
, which when divided by a thousand leaves a remainder of ![]()
-Mr.Sharkman
Note: my solution was very long and tedious. It was definitely was the least elegant solution. The only thing I like about it is it contains no quadratic equations (unless you count LoC).
Solution 7 Analytic Geometry
Let ![]() and
and ![]() be the midpoints of
be the midpoints of ![]() and
and ![]() , respectively, such that
, respectively, such that ![]() intersects
intersects ![]() .
.
Since ![]() and
and ![]() are midpoints,
are midpoints, ![]() and
and ![]() .
.
![]() and
and ![]() are located on the circumference of the circle, so
are located on the circumference of the circle, so ![]() .
.
Since ![]() and
and ![]() ,
,
![]() and
and ![]()
With law of cosines, ![]()
Since ![]() ,
, ![]() is acute angle.
is acute angle. ![]() and
and ![]()
Let ![]() line be
line be ![]() axis.
axis.
Line ![]() equation is
equation is ![]() .
.
Since line ![]() passes point
passes point ![]() and perpendicular to
and perpendicular to ![]() , its equation is
, its equation is ![]()
where ![]() ,
, ![]()
Since ![]() is the intersection of
is the intersection of ![]() and
and ![]() ,
,
![]()
![]() (Negative means point
(Negative means point ![]() is between point
is between point ![]() and
and ![]() )
)
![]() and the answer is
and the answer is ![]() .
.
Note: if ![]() was longer, point
was longer, point ![]() would be between point
would be between point ![]() and
and ![]() . Then,
. Then, ![]() would be the diagonal of quadrilateral
would be the diagonal of quadrilateral ![]() not the side. To apply Ptolemy's theorem like solution 4, it is critical to know whether
not the side. To apply Ptolemy's theorem like solution 4, it is critical to know whether ![]() is the diagonal or side of quadrilateral. Equation for wrong case cannot be solved. For example,
is the diagonal or side of quadrilateral. Equation for wrong case cannot be solved. For example,
See also
| 2011 AIME II (Problems • Answer Key • Resources) | ||
| Preceded by Problem 9 |
Followed by Problem 11 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.