Difference between revisions of "2011 AIME II Problems/Problem 15"

Revision as of 15:46, 2 June 2020

Problem

Let $P(x) = x^2 - 3x - 9$ . A real number $x$ is chosen at random from the interval $5 \le x \le 15$ . The probability that $\lfloor\sqrt{P(x)}\rfloor = \sqrt{P(\lfloor x \rfloor)}$ is equal to $\frac{\sqrt{a} + \sqrt{b} + \sqrt{c} - d}{e}$ , where $a$ , $b$ , $c$ , $d$ , and $e$ are positive integers. Find $a + b + c + d + e$ .

Solution 1

Table of values of $P(x)$ :

$\begin{align*} P(5) &= 1 \\ P(6) &= 9 \\ P(7) &= 19 \\ P(8) &= 31 \\ P(9) &= 45 \\ P(10) &= 61 \\ P(11) &= 79 \\ P(12) &= 99 \\ P(13) &= 121 \\ P(14) &= 145 \\ P(15) &= 171 \\ \end{align*}$

In order for $\lfloor \sqrt{P(x)} \rfloor = \sqrt{P(\lfloor x \rfloor)}$ to hold, $\sqrt{P(\lfloor x \rfloor)}$ must be an integer and hence $P(\lfloor x \rfloor)$ must be a perfect square. This limits $x$ to $5 \le x < 6$ or $6 \le x < 7$ or $13 \le x < 14$ since, from the table above, those are the only values of $x$ for which $P(\lfloor x \rfloor)$ is an perfect square. However, in order for $\sqrt{P(x)}$ to be rounded down to $P(\lfloor x \rfloor)$ , $P(x)$ must be less than the next perfect square after $P(\lfloor x \rfloor)$ (for the said intervals). Now, we consider the three cases:

Case $5 \le x < 6$ :

$P(x)$ must be less than the first perfect square after $1$ , which is $4$ , i.e.:

$1 \le P(x) < 4$ (because $\lfloor \sqrt{P(x)} \rfloor = 1$ implies $1 \le \sqrt{P(x)} < 2$ )

Since $P(x)$ is increasing for $x \ge 5$ , we just need to find the value $v \ge 5$ where $P(v) = 4$ , which will give us the working range $5 \le x < v$ .

$\begin{align*} v^2 - 3v - 9 &= 4 \\ v &= \frac{3 + \sqrt{61}}{2} \end{align*}$

So in this case, the only values that will work are $5 \le x < \frac{3 + \sqrt{61}}{2}$ .

Case $6 \le x < 7$ :

$P(x)$ must be less than the first perfect square after $9$ , which is $16$ .

$\begin{align*} v^2 - 3v - 9 &= 16 \\ v &= \frac{3 + \sqrt{109}}{2} \end{align*}$

So in this case, the only values that will work are $6 \le x < \frac{3 + \sqrt{109}}{2}$ .

Case $13 \le x < 14$ :

$P(x)$ must be less than the first perfect square after $121$ , which is $144$ .

$\begin{align*} v^2 - 3v - 9 &= 144 \\ v &= \frac{3 + \sqrt{621}}{2} \end{align*}$

So in this case, the only values that will work are $13 \le x < \frac{3 + \sqrt{621}}{2}$ .

Now, we find the length of the working intervals and divide it by the length of the total interval, $15 - 5 = 10$ :

$\begin{align*} \frac{\left( \frac{3 + \sqrt{61}}{2} - 5 \right) + \left( \frac{3 + \sqrt{109}}{2} - 6 \right) + \left( \frac{3 + \sqrt{621}}{2} - 13 \right)}{10} \\ &= \frac{\sqrt{61} + \sqrt{109} + \sqrt{621} - 39}{20} \end{align*}$

Thus, the answer is $61 + 109 + 621 + 39 + 20 = \fbox{850}$ .

P.S. You don't need to calculate all the values of P(x) calculated by the above solution. Some very simple modular arithmetic eliminates a large portion of the numbers. The time saved is not that much if you are already at your mathcounts prime.

Solution 2

Make the substitution $y=2x-3$ , so $P(x)=\frac{y^2-45}{4}.$ We're looking for solutions to $\bigg\lfloor{\sqrt{\frac{y^2-45}{4}}\bigg\rfloor}=\sqrt{\frac{\lfloor{y\rfloor}^2-45}{4}}$ with the new bounds $y\in{[7,27]}$ . Since the right side is an integer, it must be that $\frac{\lfloor{y\rfloor}^2-45}{4}$ is a perfect square. For simplicity, write $\lfloor{y\rfloor}=a$ and $a^2-45=4b^2\implies{(a-2b)(a+2b)=45}.$ Since $a-2b<a+2b$ , it must be that $(a-2b,a+2b)=(1,45),(3,15),(5,9)$ , which gives solutions $(23,11),(9,3),(7,1)$ , respectively. But this gives us three cases to check:

Case 1: $\bigg\lfloor{\sqrt{\frac{y^2-45}{4}}\bigg\rfloor}=11$ .

In this case, we have $11\leq{\sqrt{\frac{y^2-45}{4}}}<12\implies{y\in{[23,\sqrt{621})}}.$ Case 2: $\bigg\lfloor{\sqrt{\frac{y^2-45}{4}}\bigg\rfloor}=3$ .

In this case, we have $3\leq{\sqrt{\frac{y^2-45}{4}}}<4\implies{y\in{[9,\sqrt{109})}}.$ Case 3: $\bigg\lfloor{\sqrt{\frac{y^2-45}{4}}\bigg\rfloor}=1$

In this case, we have $1\leq{\sqrt{\frac{y^2-45}{4}}}<2\implies{y\in{[7,\sqrt{61})}}.$ To finish, the total length of the interval from which we choose $y$ is $27-7=20$ . The total length of the success intervals is $(\sqrt{61}-7)+(\sqrt{109}-9)+(\sqrt{621}-23)=\sqrt{61}+\sqrt{109}+\sqrt{621}-39,$ which means the probability is $\frac{\sqrt{61}+\sqrt{109}+\sqrt{621}-39}{20}.$ AIMEifying the answer gives $\boxed{850}$ .

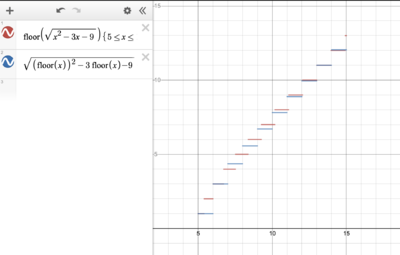
Solution 3 (Graphing)

It's definitely possible to conceptualize this problem visually, if that's your thing, since it is a geometric probability problem. Let $A = \lfloor\sqrt{P(x)}\rfloor$ and $B = \sqrt{P(\lfloor x \rfloor)}$ . The graph of $A$ and $B$ will look like this, with $A$ having only integral y-values and $B$ having only integral x-values:

As both $A$ and $B$ consist of a bunch of line segments, the probability that $A = B$ is the "length" of the overlap between the segments of $A$ and $B$ divided by the total length of the segments of $B$ .

Looking at the graph, we see that $A$ and $B$ will overlap only when $B$ is an integer. Specifically, each region of overlap will begin when $\sqrt{P(x)}\ = k, 5 \le x \le 15$ has solutions for integral $k$ in the range of $A$ , which consists of the integers $1-13$ , and end when $A$ jumps up to its next y-value.

Using the quadratic formula, we see that the start point of each of these overlapping segments will be the integral values of $\frac{3 + \sqrt{45 + 4k^2}}{2}$ for $k$ in the specified range, meaning $45 + 4k^2$ must be a perfect square. Plugging in all the possible values of $k$ , we get $k = 1, 3, 11$ , corresponding to start points of $x = 5, 6, 13$ . As already stated, the endpoints will occur when $A$ jumps up to the next integer $k$ at each of these segments, at which point the x-value will be $\frac{3 + \sqrt{45 + 4k^2}}{2}$ . On the graph, the overlapping segments of $A$ and $B$ would be represented by the highlighted green segments below:

Taking the difference between this second x-value and the start point for each of our start points $x = 5, 6, 13$ and summing them will give us the total length of these green segments. We can then divide this value by ten (the total length of the segments of $B$ ) to give us the probability of overlap between $A$ and $B$ .

Doing so gives us:

$\frac{\left( \frac{3 + \sqrt{61}}{2} - 5 \right) + \left( \frac{3 + \sqrt{109}}{2} - 6 \right) + \left( \frac{3 + \sqrt{621}}{2} - 13 \right)}{10} = \frac{\sqrt{61} + \sqrt{109} + \sqrt{621} - 39}{20}$

$\implies{61 + 109 + 621 + 39 + 20 = \fbox{850}}$ .

~ anellipticcurveoverq

Solution 4

Note that all the "bounds" have to be less than the number+1, otherwise it wouldn't fit the answer format. Therefore, the answer is $\frac{3*3+\sqrt{9+4(4+9)}-10+\sqrt{9+4(16+9)}-12+\sqrt{9+4(144+9)}}{20} \implies \boxed{850}$

~Lcz

@@ Line 111: / Line 111: @@
 ~ anellipticcurveoverq
+==Solution 4==
+Note that all the "bounds" have to be less than the number+1, otherwise it wouldn't fit the answer format. Therefore, the answer is <math>\frac{3*3+\sqrt{9+4(4+9)}-10+\sqrt{9+4(16+9)}-12+\sqrt{9+4(144+9)}}{20} \implies \boxed{850}</math>
+~Lcz
 ==See also==

2011 AIME II (Problems • Answer Key • Resources)
Preceded by Problem 14	Followed by Last Problem
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

Page

Toolbox

Search