Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2011 AMC 10B Problems/Problem 22"

m
m
Line 56: Line 56:
  
 
The volume of the cube is <math>s^3 = (\sqrt{2}-1)^3 = (\sqrt{2}-1)(3-2\sqrt{2}) = 3\sqrt{2}-3-4+2\sqrt{2} = \boxed{\textbf{(A)} 5\sqrt{2}-7}</math>
 
The volume of the cube is <math>s^3 = (\sqrt{2}-1)^3 = (\sqrt{2}-1)(3-2\sqrt{2}) = 3\sqrt{2}-3-4+2\sqrt{2} = \boxed{\textbf{(A)} 5\sqrt{2}-7}</math>
 +
 +
== See Also==
 +
 +
{{AMC10 box|year=2011|ab=B|num-b=21|num-a=23}}

Revision as of 19:51, 4 June 2011

Problem 22

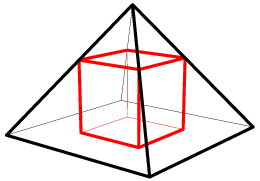
A pyramid has a square base with sides of length $1$ and has lateral faces that are equilateral triangles. A cube is placed within the pyramid so that one face is on the base of the pyramid and its opposite face has all its edges on the lateral faces of the pyramid. What is the volume of this cube?

$\textbf{(A)}\ 5\sqrt{2} - 7 \qquad\textbf{(B)}\ 7 - 4\sqrt{3} \qquad\textbf{(C)}\ \frac{2\sqrt{2}}{27} \qquad\textbf{(D)}\ \frac{\sqrt{2}}{9} \qquad\textbf{(E)}\ \frac{\sqrt{3}}{9}$

Solution

It is often easier to first draw a diagram for such a problem.

2011AMC10B22.png

Sometimes, it may also be easier to think of the problem in 2D. Take a cross section of the pyramid through the apex and two points from the base that are opposite to each other. Place it in two dimensions.

[asy] unitsize(35mm); defaultpen(linewidth(2pt)+fontsize(10pt)); pair A=(0,0), B=(sqrt(2),0), C=(0.5sqrt(2),0.5sqrt(2)); pair W=(sqrt(2)-1,0), X=(1,0), Y=(1,sqrt(2)-1), Z=(sqrt(2)-1,sqrt(2)-1); draw(A--B--C--cycle); draw(W--X--Y--Z--cycle,red); [/asy]

The dimensions of this triangle are $1, 1,$ and $\sqrt{2}$ because the sidelengths of the pyramid are $1$ and the base of the triangle is the diagonal of the pyramid's base. This is a $45-45-90$ triangle. Also, we can let the dimensions of the rectangle be $s$ and $s\sqrt{2}$ because the longer side was the diagonal of the cube's base and the shorter cube was a side of the cube.

[asy] unitsize(35mm); defaultpen(linewidth(2pt)+fontsize(12pt)); pair A=(0,0), B=(sqrt(2),0), C=(0.5sqrt(2),0.5sqrt(2)); pair W=(sqrt(2)-1,0), X=(1,0), Y=(1,sqrt(2)-1), Z=(sqrt(2)-1,sqrt(2)-1); draw(A--B--C--cycle); draw(W--X--Y--Z--cycle,red); label("$1$",(A--C),NW); label("$1$",(B--C),NE); label("$\sqrt{2}$",(A--B),S); label("$s$",(W--Z),E,red); label("$s$",(X--Y),W,red); label("$s\sqrt{2}$",(W--X),N,red); [/asy]

The two triangles on the right and left of the rectangle are also $45-45-90$ triangles because the rectangle is perpendicular to the base, and they share a $45^\circ$ angle with the larger triangle. Therefore, the legs of the right triangles can be expressed as $s.$

[asy] unitsize(35mm); defaultpen(linewidth(2pt)+fontsize(12pt)); pair A=(0,0), B=(sqrt(2),0), C=(0.5sqrt(2),0.5sqrt(2)); pair W=(sqrt(2)-1,0), X=(1,0), Y=(1,sqrt(2)-1), Z=(sqrt(2)-1,sqrt(2)-1); draw(A--B--C--cycle); draw(W--X--Y--Z--cycle,red); label("$1$",(A--C),NW); label("$1$",(B--C),NE); label("$\sqrt{2}$",(A--B),S); label("$s$",(W--Z),E,red); label("$s$",(X--Y),W,red); label("$s\sqrt{2}$",(W--X),N,red); label("$s$",(A--W),N); label("$s$",(X--B),N); [/asy]

Now we can just use segment addition to find the value of $s.$ \[\sqrt{2}=s+s\sqrt{2}+s=2s+s\sqrt{2}=(2+\sqrt{2})s\] \[s=\frac{\sqrt{2}}{2+\sqrt{2}}=\frac{1}{\sqrt{2}+1}=\frac{\sqrt{2}-1}{2-1}=\sqrt{2}-1\]

The volume of the cube is $s^3 = (\sqrt{2}-1)^3 = (\sqrt{2}-1)(3-2\sqrt{2}) = 3\sqrt{2}-3-4+2\sqrt{2} = \boxed{\textbf{(A)} 5\sqrt{2}-7}$

See Also

2011 AMC 10B (Problems • Answer Key • Resources)
Preceded by
Problem 21 		Followed by
Problem 23
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions
Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2011_AMC_10B_Problems/Problem_22&oldid=39187"