2011 AMC 10B Problems/Problem 22
Problem
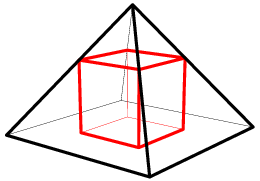
A pyramid has a square base with sides of length ![]() and has lateral faces that are equilateral triangles. A cube is placed within the pyramid so that one face is on the base of the pyramid and its opposite face has all its edges on the lateral faces of the pyramid. What is the volume of this cube?
and has lateral faces that are equilateral triangles. A cube is placed within the pyramid so that one face is on the base of the pyramid and its opposite face has all its edges on the lateral faces of the pyramid. What is the volume of this cube?
![]()
Solution
It is often easier to first draw a diagram for such a problem.
Sometimes, it may also be easier to think of the problem in 2D. Take a cross section of the pyramid through the apex and two points from the base that are opposite to each other. Place it in two dimensions.
![[asy] unitsize(35mm); defaultpen(linewidth(2pt)+fontsize(10pt)); pair A=(0,0), B=(sqrt(2),0), C=(0.5sqrt(2),0.5sqrt(2)); pair W=(sqrt(2)-1,0), X=(1,0), Y=(1,sqrt(2)-1), Z=(sqrt(2)-1,sqrt(2)-1); draw(A--B--C--cycle); draw(W--X--Y--Z--cycle,red); [/asy]](http://latex.artofproblemsolving.com/2/1/5/215607fef86013352901dcb40b988542f35becbf.png)
The dimensions of this triangle are ![]() and
and ![]() because the sidelengths of the pyramid are
because the sidelengths of the pyramid are ![]() and the base of the triangle is the diagonal of the pyramid's base. This is a
and the base of the triangle is the diagonal of the pyramid's base. This is a ![]() triangle. Also, we can let the dimensions of the rectangle be
triangle. Also, we can let the dimensions of the rectangle be ![]() and
and ![]() because the longer side was the diagonal of the cube's base and the shorter cube was a side of the cube.
because the longer side was the diagonal of the cube's base and the shorter cube was a side of the cube.
![[asy] unitsize(35mm); defaultpen(linewidth(2pt)+fontsize(12pt)); pair A=(0,0), B=(sqrt(2),0), C=(0.5sqrt(2),0.5sqrt(2)); pair W=(sqrt(2)-1,0), X=(1,0), Y=(1,sqrt(2)-1), Z=(sqrt(2)-1,sqrt(2)-1); draw(A--B--C--cycle); draw(W--X--Y--Z--cycle,red); label("$1$",(A--C),NW); label("$1$",(B--C),NE); label("$\sqrt{2}$",(A--B),S); label("$s$",(W--Z),E,red); label("$s$",(X--Y),W,red); label("$s\sqrt{2}$",(W--X),N,red); [/asy]](http://latex.artofproblemsolving.com/c/3/6/c360ad03631afaf0bd9850333d36ecfc30161c02.png)
The two triangles on the right and left of the rectangle are also ![]() triangles because the rectangle is perpendicular to the base, and they share a
triangles because the rectangle is perpendicular to the base, and they share a ![]() angle with the larger triangle. Therefore, the legs of the right triangles can be expressed as
angle with the larger triangle. Therefore, the legs of the right triangles can be expressed as ![]()
![[asy] unitsize(35mm); defaultpen(linewidth(2pt)+fontsize(12pt)); pair A=(0,0), B=(sqrt(2),0), C=(0.5sqrt(2),0.5sqrt(2)); pair W=(sqrt(2)-1,0), X=(1,0), Y=(1,sqrt(2)-1), Z=(sqrt(2)-1,sqrt(2)-1); draw(A--B--C--cycle); draw(W--X--Y--Z--cycle,red); label("$1$",(A--C),NW); label("$1$",(B--C),NE); label("$\sqrt{2}$",(A--B),S); label("$s$",(W--Z),E,red); label("$s$",(X--Y),W,red); label("$s\sqrt{2}$",(W--X),N,red); label("$s$",(A--W),N); label("$s$",(X--B),N); [/asy]](http://latex.artofproblemsolving.com/d/0/d/d0dbfd874b642e9b3edf55e50e44d677f4eed432.png)
Now we can just use segment addition to find the value of ![]()
![]()
![]()
The volume of the cube is ![]()
Umm.... Above, yeah... that's all wrong. The triangle when put in 2d is an equilateral triangle, not a right triangle. and the "rectangle" in 2d
should be a square. Sooo yeah don't listen to that. But the answer is right, it is A. Hmm... wonder why :)
That above comment seems to be wrong (I'm probably not supposed to delete it), most likely due to the fact that the person who wrote it failed to notice that the cross-section was made diagonally rather than however he/she thought it was made.