Difference between revisions of "2011 AMC 10B Problems/Problem 25"
(→See Also) |
m (→Solution 1) |
||
| (41 intermediate revisions by 20 users not shown) | |||
| Line 1: | Line 1: | ||
== Problem == | == Problem == | ||
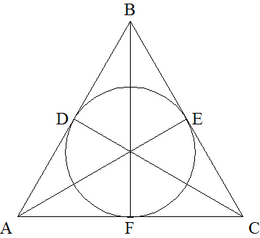
| − | Let <math>T_1</math> be a triangle with | + | Let <math>T_1</math> be a triangle with side lengths <math>2011, 2012,</math> and <math>2013</math>. For <math>n \ge 1</math>, if <math>T_n = \triangle ABC</math> and <math>D, E,</math> and <math>F</math> are the points of tangency of the incircle of <math>\triangle ABC</math> to the sides <math>AB, BC</math>, and <math>AC,</math> respectively, then <math>T_{n+1}</math> is a triangle with side lengths <math>AD, BE,</math> and <math>CF,</math> if it exists. What is the perimeter of the last triangle in the sequence <math>( T_n )</math>? |
<math> \textbf{(A)}\ \frac{1509}{8} \qquad\textbf{(B)}\ \frac{1509}{32} \qquad\textbf{(C)}\ \frac{1509}{64} \qquad\textbf{(D)}\ \frac{1509}{128} \qquad\textbf{(E)}\ \frac{1509}{256}</math> | <math> \textbf{(A)}\ \frac{1509}{8} \qquad\textbf{(B)}\ \frac{1509}{32} \qquad\textbf{(C)}\ \frac{1509}{64} \qquad\textbf{(D)}\ \frac{1509}{128} \qquad\textbf{(E)}\ \frac{1509}{256}</math> | ||
| + | [[Category: Introductory Geometry Problems]] | ||
| − | ==Solution== | + | ==Solution 1== |
| − | + | ||
By constructing the bisectors of each angle and the perpendicular radii of the incircle the triangle consists of 3 kites. | By constructing the bisectors of each angle and the perpendicular radii of the incircle the triangle consists of 3 kites. | ||
| Line 23: | Line 24: | ||
Solving gives: | Solving gives: | ||
| − | <math>x= \frac{a}{2} - 1</math> | + | <math>x= \frac{a}{2} -1</math> |
<math>y = \frac{a}{2}</math> | <math>y = \frac{a}{2}</math> | ||
| Line 31: | Line 32: | ||
Subbing in gives that <math>T_2</math> has sides of <math>1005, 1006, 1007</math>. | Subbing in gives that <math>T_2</math> has sides of <math>1005, 1006, 1007</math>. | ||
| − | <math>T_3</math> can easily be | + | <math>T_3</math> can easily be derived from this as the sides still differ by 1 hence the above solutions still work (now with <math>a=1006</math>). All additional triangles will differ by one as the solutions above differ by one so this process can be repeated indefinitely until the side lengths no longer form a triangle. |
Subbing in gives <math>T_3</math> with sides <math>502, 503, 504</math>. | Subbing in gives <math>T_3</math> with sides <math>502, 503, 504</math>. | ||
| Line 49: | Line 50: | ||
<math>T_{10}</math> has sides <math>\frac{375}{128}, \frac{503}{128}, \frac{631}{128}</math>. | <math>T_{10}</math> has sides <math>\frac{375}{128}, \frac{503}{128}, \frac{631}{128}</math>. | ||
| − | <math>T_{11}</math> would have sides <math>\frac{247}{256}, \frac{503}{256}, \frac{759}{256}</math> but these | + | <math>T_{11}</math> would have sides <math>\frac{247}{256}, \frac{503}{256}, \frac{759}{256}</math> but these lengths do not make a |
| − | triangle as < | + | triangle as |
| + | <cmath>\frac{247}{256} + \frac{503}{256} < \frac{759}{256}</cmath> | ||
| + | |||
| + | |||
| + | Likewise, you could create an equation instead of listing all the triangles to <math>T_{11}</math>. | ||
| + | The sides of a triangle <math>T_{k}</math> would be | ||
| + | <cmath>\frac{503}{2^{k-3}} - 1, \frac{503}{2^{k-3}}, \frac{503}{2^{k-3}} + 1</cmath> | ||
| + | We then have | ||
| + | <cmath>503 - 2^{k-3} + 503 > 503 + 2^{k-3}</cmath> | ||
| + | <cmath>1006 - 2^{k-3} > 503 + 2^{k-3}</cmath> | ||
| + | <cmath>503 > 2^{k-2}</cmath> | ||
| + | <cmath>9 > k-2</cmath> | ||
| + | <cmath>k < 11</cmath> | ||
| + | Hence, the first triangle which does not exist in this sequence is <math>T_{11}</math>. | ||
| + | |||
| + | Hence the perimeter is | ||
| + | <cmath>\frac{375}{128} + \frac{503}{128} + \frac{631}{128} = \boxed{\textbf{(D)} \frac{1509}{128}}</cmath>. | ||
| − | + | ==Solution 2== | |
| − | + | ||
| + | Proceeding similarly to the first solution, we have that sides of each triangle are of the form <math>a, a+1, a+2</math> for some number <math>a</math>. Also, note that the perimeter of each triangle is half of the previous one. In order for the triangle to not exist, it must not satisfy the triangle inequality, meaning that <math>a + a + 1 < a+2 \Rightarrow a<1</math>. Then, the perimeter would be <math>a + a + 1 + a + 2 = 3a + 3 < 6</math>. So, to have a proper triangle, we have <math>\frac{3018}{2^{k}} > 6 \Rightarrow 2^k < 503 \Rightarrow 2^{k} \leq 512</math>. The first triangle to not work would have perimeter <math>\frac{3018}{512} = \frac{1509}{256}</math>, thus the answer is <math>\boxed{\textbf{(D)} \frac{1509}{128}}</math>. | ||
==See Also== | ==See Also== | ||
| − | + | Identical problem to the [[2011 AMC 12B Problems/Problem 22]]. | |
{{AMC10 box|year=2011|ab=B|num-b=24|after=Last Problem}} | {{AMC10 box|year=2011|ab=B|num-b=24|after=Last Problem}} | ||
| + | {{MAA Notice}} | ||
Latest revision as of 03:15, 3 November 2022
Contents
Problem
Let ![]() be a triangle with side lengths
be a triangle with side lengths ![]() and
and ![]() . For
. For ![]() , if
, if ![]() and
and ![]() and
and ![]() are the points of tangency of the incircle of
are the points of tangency of the incircle of ![]() to the sides
to the sides ![]() , and
, and ![]() respectively, then
respectively, then ![]() is a triangle with side lengths
is a triangle with side lengths ![]() and
and ![]() if it exists. What is the perimeter of the last triangle in the sequence
if it exists. What is the perimeter of the last triangle in the sequence ![]() ?
?
![]()
Solution 1
By constructing the bisectors of each angle and the perpendicular radii of the incircle the triangle consists of 3 kites.
Hence ![]() and
and ![]() and
and ![]() . Let
. Let ![]() and
and ![]() gives three equations:
gives three equations:
![]()
![]()
![]()
(where ![]() for the first triangle.)
for the first triangle.)
Solving gives:
![]()
![]()
![]()
Subbing in gives that ![]() has sides of
has sides of ![]() .
.
![]() can easily be derived from this as the sides still differ by 1 hence the above solutions still work (now with
can easily be derived from this as the sides still differ by 1 hence the above solutions still work (now with ![]() ). All additional triangles will differ by one as the solutions above differ by one so this process can be repeated indefinitely until the side lengths no longer form a triangle.
). All additional triangles will differ by one as the solutions above differ by one so this process can be repeated indefinitely until the side lengths no longer form a triangle.
Subbing in gives ![]() with sides
with sides ![]() .
.
![]() has sides
has sides ![]() .
.
![]() has sides
has sides ![]() .
.
![]() has sides
has sides ![]() .
.
![]() has sides
has sides ![]() .
.
![]() has sides
has sides ![]() .
.
![]() has sides
has sides ![]() .
.
![]() has sides
has sides ![]() .
.
![]() would have sides
would have sides ![]() but these lengths do not make a
triangle as
but these lengths do not make a
triangle as
![]()
Likewise, you could create an equation instead of listing all the triangles to ![]() .
The sides of a triangle
.
The sides of a triangle ![]() would be
would be
![]() We then have
We then have
![]()
![]()
![]()
![]()
![]() Hence, the first triangle which does not exist in this sequence is
Hence, the first triangle which does not exist in this sequence is ![]() .
.
Hence the perimeter is
![]() .
.
Solution 2
Proceeding similarly to the first solution, we have that sides of each triangle are of the form ![]() for some number
for some number ![]() . Also, note that the perimeter of each triangle is half of the previous one. In order for the triangle to not exist, it must not satisfy the triangle inequality, meaning that
. Also, note that the perimeter of each triangle is half of the previous one. In order for the triangle to not exist, it must not satisfy the triangle inequality, meaning that ![]() . Then, the perimeter would be
. Then, the perimeter would be ![]() . So, to have a proper triangle, we have
. So, to have a proper triangle, we have ![]() . The first triangle to not work would have perimeter
. The first triangle to not work would have perimeter ![]() , thus the answer is
, thus the answer is ![]() .
.
See Also
Identical problem to the 2011 AMC 12B Problems/Problem 22.
| 2011 AMC 10B (Problems • Answer Key • Resources) | ||
| Preceded by Problem 24 |
Followed by Last Problem | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.