2012 AMC 12B Problems/Problem 19
Solution
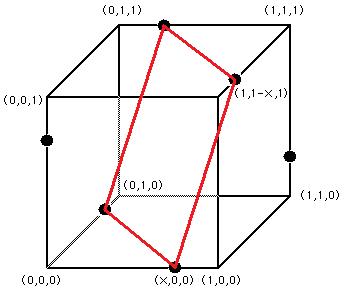
Observe the diagram above. Each dot represents one of the six vertices of the regular octahedron. Three dots have been placed exactly x units from the (0,0,0) corner of the unit cube. The other three dots have been placed exactly x units from the (1,1,1) corner of the unit cube. A red square has been drawn connecting four of the dots to provide perspective regarding the shape of the octahedron. Observe that the three dots that are near (0,0,0) are each x*sqrt(2) from each other. The same is true for the three dots that are near (1,1,1). There is a unique x for which the rectangle drawn in red becomes a square. This will occur when the distance from (x,0,0) to (1,1-x, 1) is x*sqrt(2).
Using the distance formula we find the distance between the two points to be: sqrt((1-x)^2 + (1-x)^2 + 1) = sqrt(2x^2 - 4x +3). Equating this to x*sqrt(2) and squaring both sides, we have the equation:
2x^2 - 4x + 3 = 2x^2
-4x + 3 = 0
x = 3/4.
Since the length of each side is x*sqrt(2), we have a final result of 3sqrt(2)/4. Thus, Answer choice A is correct.
(If someone can draw a better diagram with the points labeled P1,P2, etc., I would appreciate it).
--Jm314 14:55, 26 February 2012 (EST)