Difference between revisions of "2013 AIME II Problems/Problem 10"
(Tag: Undo) |
m (→Solution 1 (Coordbash)) |
||
| (11 intermediate revisions by 8 users not shown) | |||
| Line 1: | Line 1: | ||
| − | ==Problem | + | ==Problem== |
| + | |||
Given a circle of radius <math>\sqrt{13}</math>, let <math>A</math> be a point at a distance <math>4 + \sqrt{13}</math> from the center <math>O</math> of the circle. Let <math>B</math> be the point on the circle nearest to point <math>A</math>. A line passing through the point <math>A</math> intersects the circle at points <math>K</math> and <math>L</math>. The maximum possible area for <math>\triangle BKL</math> can be written in the form <math>\frac{a - b\sqrt{c}}{d}</math>, where <math>a</math>, <math>b</math>, <math>c</math>, and <math>d</math> are positive integers, <math>a</math> and <math>d</math> are relatively prime, and <math>c</math> is not divisible by the square of any prime. Find <math>a+b+c+d</math>. | Given a circle of radius <math>\sqrt{13}</math>, let <math>A</math> be a point at a distance <math>4 + \sqrt{13}</math> from the center <math>O</math> of the circle. Let <math>B</math> be the point on the circle nearest to point <math>A</math>. A line passing through the point <math>A</math> intersects the circle at points <math>K</math> and <math>L</math>. The maximum possible area for <math>\triangle BKL</math> can be written in the form <math>\frac{a - b\sqrt{c}}{d}</math>, where <math>a</math>, <math>b</math>, <math>c</math>, and <math>d</math> are positive integers, <math>a</math> and <math>d</math> are relatively prime, and <math>c</math> is not divisible by the square of any prime. Find <math>a+b+c+d</math>. | ||
| − | ==Solution 1== | + | ==Solution 1 (Coordbash)== |
<asy> | <asy> | ||
import math; | import math; | ||
| Line 33: | Line 34: | ||
Also, the distance between <math>B</math> and <math>LK</math> is <math>\frac{k\times \sqrt{13}-(4+\sqrt{13})\cdot k}{\sqrt{1+k^2}}=\frac{-4k}{\sqrt{1+k^2}}</math> | Also, the distance between <math>B</math> and <math>LK</math> is <math>\frac{k\times \sqrt{13}-(4+\sqrt{13})\cdot k}{\sqrt{1+k^2}}=\frac{-4k}{\sqrt{1+k^2}}</math> | ||
| − | So the area <math>S=0.5ah=\frac{-4k\sqrt{(16 | + | So the area <math>S=0.5ah=\frac{-4k\sqrt{(16+8\sqrt{13})k^2-13}}{k^2+1}</math> |
Then the maximum value of <math>S</math> is <math>\frac{104-26\sqrt{13}}{3}</math> | Then the maximum value of <math>S</math> is <math>\frac{104-26\sqrt{13}}{3}</math> | ||
| Line 67: | Line 68: | ||
So when area of <math>\triangle OKL</math> is maximized, <math>\angle KOL = \frac{\pi}{2}</math>. | So when area of <math>\triangle OKL</math> is maximized, <math>\angle KOL = \frac{\pi}{2}</math>. | ||
| − | Eventually, we get <cmath>\triangle BKL= | + | Eventually, we get <cmath>\triangle BKL= \frac12 \cdot (\sqrt{13})^2\cdot(\frac{4}{4+\sqrt{13}})=\frac{104-26\sqrt{13}}{3}</cmath> |
So the answer is <math>104+26+13+3=\boxed{146}</math>. | So the answer is <math>104+26+13+3=\boxed{146}</math>. | ||
| + | |||
| + | ==Solution 3 (simpler solution)== | ||
| + | A rather easier solution is presented in the Girls' Angle WordPress: | ||
| + | |||
| + | http://girlsangle.wordpress.com/2013/11/26/2013-aime-2-problem-10/ | ||
| + | |||
| + | |||
| + | ==Solution 4== | ||
| + | |||
| + | Let <math>N,M</math> les on <math>AL</math> such that <math>BM\bot AL, ON\bot AL</math>, call <math>BM=h, ON=k,LN=KN=d</math> We call <math>\angle{LON}=\alpha</math> By similar triangle, we have <math>\frac{h}{k}=\frac{4}{4+\sqrt{13}}, h=\frac{4k}{4+\sqrt{13}}</math>. Then, we realize the area is just <math>dh=d\cdot \frac{4K}{4+\sqrt{13}}</math> As <math>\sin \alpha=\frac{d}{\sqrt{13}}, \cos \alpha=\frac{k}{\sqrt{13}}</math>. Now, we have to maximize <math>\frac{52\sin \alpha \cos \alpha}{4+\sqrt{13}}=\frac{26\sin 2\alpha}{4+\sqrt{13}}</math>, which is obviously reached when <math>\alpha=45^{\circ}</math>, the answer is <math>\frac{104-26\sqrt{13}}{3}</math> leads to <math>\boxed{146}</math> | ||
| + | |||
| + | ~bluesoul | ||
| + | |||
| + | ==Solution 5== | ||
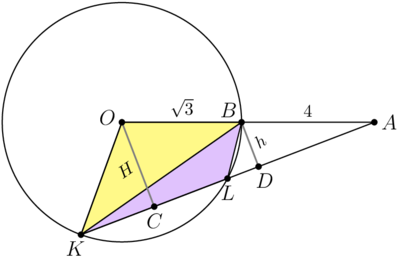
| + | [[File:AIME-II-2013-10.png|400px|right]] | ||
| + | Let C and D be the base of perpendiculars dropped from points O and B to AK. Denote BD = h, OC = H. | ||
| + | <cmath>\triangle ABD \sim \triangle AOC \implies \frac {h}{H} = \frac {4}{4 + \sqrt{13}}.</cmath> | ||
| + | <math>KL</math> is the base of triangles <math>\triangle OKL</math> and <math>\triangle BKL \implies \frac {[BKL]}{[OKL]} = \frac{h}{H} =</math> const <math>\implies</math> | ||
| + | The maximum possible area for <math>\triangle BKL</math> and <math>\triangle OKL</math> are at the same position of point <math>K</math>. | ||
| + | |||
| + | <math>\triangle OKL</math> has sides <math>OK = OL = \sqrt{13}\implies \max[\triangle OKL] = \frac {OK^2}{2} = \frac {13}{2}</math> | ||
| + | |||
| + | in the case <math>\angle KOL = 90^\circ.</math> It is possible – if we rotate such triangle, we can find position when <math>A</math> lies on <math>KL.</math> | ||
| + | <cmath>\max[\triangle BKL] = \max[\triangle OKL] \cdot \frac {4}{4+\sqrt{13}} = \frac {26}{4+\sqrt{13}} \implies \boxed{\textbf{146}}</cmath> | ||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
==See Also== | ==See Also== | ||
| − | |||
{{AIME box|year=2013|n=II|num-b=9|num-a=11}} | {{AIME box|year=2013|n=II|num-b=9|num-a=11}} | ||
{{MAA Notice}} | {{MAA Notice}} | ||
Latest revision as of 17:57, 29 December 2023
Contents
Problem
Given a circle of radius ![]() , let
, let ![]() be a point at a distance
be a point at a distance ![]() from the center
from the center ![]() of the circle. Let
of the circle. Let ![]() be the point on the circle nearest to point
be the point on the circle nearest to point ![]() . A line passing through the point
. A line passing through the point ![]() intersects the circle at points
intersects the circle at points ![]() and
and ![]() . The maximum possible area for
. The maximum possible area for ![]() can be written in the form
can be written in the form ![]() , where
, where ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are positive integers,
are positive integers, ![]() and
and ![]() are relatively prime, and
are relatively prime, and ![]() is not divisible by the square of any prime. Find
is not divisible by the square of any prime. Find ![]() .
.
Solution 1 (Coordbash)
![[asy] import math; import olympiad; import graph; pair A, B, K, L; B = (sqrt(13), 0); A=(4+sqrt(13), 0); dot(B); dot(A); draw(Circle((0,0), sqrt(13))); label("$O$", (0,0), S);label("$B$", B, SW);label("$A$", A, S); dot((0,0)); [/asy]](http://latex.artofproblemsolving.com/f/4/1/f419c223647108f3ec0e7539c755b1fef842ed2d.png)
Now we put the figure in the Cartesian plane, let the center of the circle ![]() , then
, then ![]() , and
, and ![]()
The equation for Circle O is ![]() , and let the slope of the line
, and let the slope of the line![]() be
be ![]() , then the equation for line
, then the equation for line![]() is
is ![]() .
.
Then we get ![]() . According to Vieta's Formulas, we get
. According to Vieta's Formulas, we get
![]() , and
, and ![]()
So, ![]()
Also, the distance between ![]() and
and ![]() is
is ![]()
So the area 
Then the maximum value of ![]() is
is ![]()
So the answer is ![]() .
.
Solution 2
![[asy] import math; import olympiad; import graph; pair A, B, K, L; B = (sqrt(13), 0); A=(4+sqrt(13), 0); dot(B); dot(A); draw(Circle((0,0), sqrt(13))); label("$O$", (0,0), S);label("$B$", B, SW);label("$A$", A, S); dot((0,0)); [/asy]](http://latex.artofproblemsolving.com/f/4/1/f419c223647108f3ec0e7539c755b1fef842ed2d.png)
Draw ![]() perpendicular to
perpendicular to ![]() at
at ![]() . Draw
. Draw ![]() perpendicular to
perpendicular to ![]() at
at ![]() .
.
![]()
Therefore, to maximize area of ![]() , we need to maximize area of
, we need to maximize area of ![]() .
.
![]()
So when area of ![]() is maximized,
is maximized, ![]() .
.
Eventually, we get ![]()
So the answer is ![]() .
.
Solution 3 (simpler solution)
A rather easier solution is presented in the Girls' Angle WordPress:
http://girlsangle.wordpress.com/2013/11/26/2013-aime-2-problem-10/
Solution 4
Let ![]() les on
les on ![]() such that
such that ![]() , call
, call ![]() We call
We call ![]() By similar triangle, we have
By similar triangle, we have ![]() . Then, we realize the area is just
. Then, we realize the area is just ![]() As
As ![]() . Now, we have to maximize
. Now, we have to maximize ![]() , which is obviously reached when
, which is obviously reached when ![]() , the answer is
, the answer is ![]() leads to
leads to ![]()
~bluesoul
Solution 5
Let C and D be the base of perpendiculars dropped from points O and B to AK. Denote BD = h, OC = H.
![]()
![]() is the base of triangles
is the base of triangles ![]() and
and ![]() const
const ![]() The maximum possible area for
The maximum possible area for ![]() and
and ![]() are at the same position of point
are at the same position of point ![]() .
.
![]() has sides
has sides ![]()
in the case ![]() It is possible – if we rotate such triangle, we can find position when
It is possible – if we rotate such triangle, we can find position when ![]() lies on
lies on ![]()
![]() vladimir.shelomovskii@gmail.com, vvsss
vladimir.shelomovskii@gmail.com, vvsss
See Also
| 2013 AIME II (Problems • Answer Key • Resources) | ||
| Preceded by Problem 9 |
Followed by Problem 11 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.