Difference between revisions of "2013 AIME I Problems/Problem 13"
(→Solution) |
|||
| Line 10: | Line 10: | ||
triangle <math>\Delta AB_0C_0 </math>, <math> \overline{AC_1} = 25 - \dfrac{17^2}{25} = \dfrac{25^2 - 17^2}{25} </math>. Therefore, the scale factor <math> \Delta AB_1C_1 </math> to <math>\Delta AB_0C_0 </math> is <math> \dfrac{25^2 - 17^2}{25^2}</math> , which yields the length of <math> \overline{B_1C_1} </math> as <math> \dfrac{25^2 - 17^2}{25^2}(17)</math>. | triangle <math>\Delta AB_0C_0 </math>, <math> \overline{AC_1} = 25 - \dfrac{17^2}{25} = \dfrac{25^2 - 17^2}{25} </math>. Therefore, the scale factor <math> \Delta AB_1C_1 </math> to <math>\Delta AB_0C_0 </math> is <math> \dfrac{25^2 - 17^2}{25^2}</math> , which yields the length of <math> \overline{B_1C_1} </math> as <math> \dfrac{25^2 - 17^2}{25^2}(17)</math>. | ||
Therefore, the scale factor for <math> \Delta B_1C_2C_1 </math> to <math> \Delta B_0C_1C_0 </math> is <math> \dfrac{25^2 - 17^2}{25^2} </math>. Some more algebraic manipulation will show that <math> \Delta B_nC_{n+1}C_n </math> to <math> \Delta B_{n-1}C_nC_{n-1} </math> is still <math> \dfrac{25^2 - 17^2}{25^2} </math>. Also, since the triangles are disjoint, the area of the union is the sum of the areas. Therefore, the area is the geometric series | Therefore, the scale factor for <math> \Delta B_1C_2C_1 </math> to <math> \Delta B_0C_1C_0 </math> is <math> \dfrac{25^2 - 17^2}{25^2} </math>. Some more algebraic manipulation will show that <math> \Delta B_nC_{n+1}C_n </math> to <math> \Delta B_{n-1}C_nC_{n-1} </math> is still <math> \dfrac{25^2 - 17^2}{25^2} </math>. Also, since the triangles are disjoint, the area of the union is the sum of the areas. Therefore, the area is the geometric series | ||
| − | <math> \dfrac{90 \cdot 17^2}{25} \sum_{n=0}^{\infty} (\dfrac{25^2-17^2}{25^2})^2 </math> | + | <math> \dfrac{90 \cdot 17^2}{25^2} \sum_{n=0}^{\infty} (\dfrac{25^2-17^2}{25^2})^2 </math> |
At this point, it may be wise to "simplify" <math> 25^2 - 17^2 = (25-17)(25+17) = (8)(42) = 336</math>. | At this point, it may be wise to "simplify" <math> 25^2 - 17^2 = (25-17)(25+17) = (8)(42) = 336</math>. | ||
So the geometric series converges to | So the geometric series converges to | ||
| − | <math>\dfrac{90 \cdot 17^2}{25} \dfrac{1}{1 - \dfrac{336^2}{625^2}} = \dfrac{90 \cdot 17^2}{25} \dfrac{625^2}{625^2 - 336^2}</math>. | + | <math>\dfrac{90 \cdot 17^2}{25^2} \dfrac{1}{1 - \dfrac{336^2}{625^2}} = \dfrac{90 \cdot 17^2}{25^2} \dfrac{625^2}{625^2 - 336^2}</math>. |
| − | Using the diffference of squares, we get <math>\dfrac{90 \cdot 17^2}{25}\dfrac{625^2}{(625 - 336)(625 + 336)}</math>, which simplifies to <math> \dfrac{90 \cdot 17^2}{25} \dfrac{625^2}{(289)(961)}</math>. Cancellling all common factors, we get the reduced fraction, <math> = \dfrac{90 \cdot 25^ | + | Using the diffference of squares, we get <math>\dfrac{90 \cdot 17^2}{25^2}\dfrac{625^2}{(625 - 336)(625 + 336)}</math>, which simplifies to <math> \dfrac{90 \cdot 17^2}{25^2} \dfrac{625^2}{(289)(961)}</math>. Cancellling all common factors, we get the reduced fraction, <math> = \dfrac{90 \cdot 25^2}{31^2} </math>, yielding the answer <math>961</math>. |
[[File:AIME13.png]] | [[File:AIME13.png]] | ||
Revision as of 03:08, 1 February 2014
Problem 13
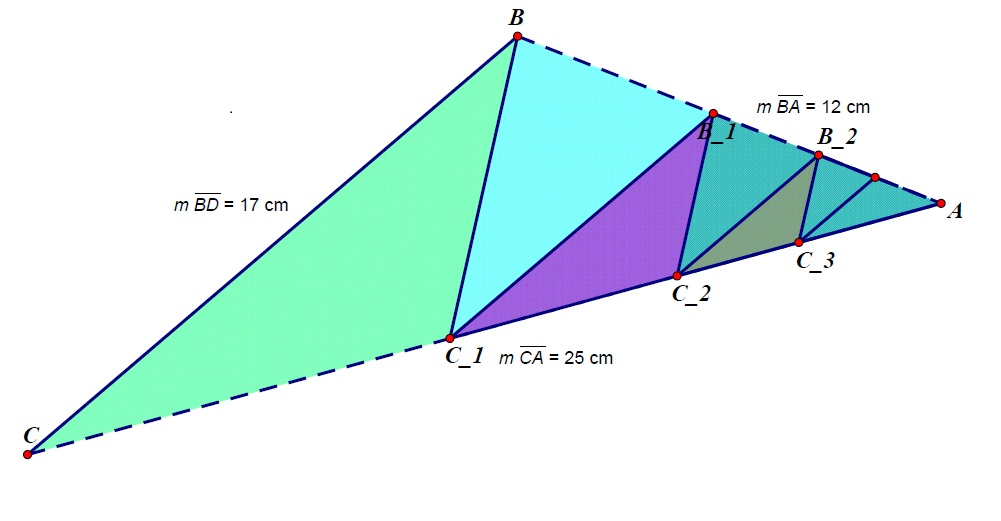
Triangle ![]() has side lengths
has side lengths ![]() ,
, ![]() , and
, and ![]() . For each positive integer
. For each positive integer ![]() , points
, points ![]() and
and ![]() are located on
are located on ![]() and
and ![]() , respectively, creating three similar triangles
, respectively, creating three similar triangles ![]() . The area of the union of all triangles
. The area of the union of all triangles ![]() for
for ![]() can be expressed as
can be expressed as ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]() .
.
Solution
(solution)
Using Heron's Formula we can get the area of the triangle ![]() . Since
. Since ![]() then the scale factor for the dimensions of
then the scale factor for the dimensions of ![]() to
to ![]() is
is ![]() Therefore, the area of
Therefore, the area of ![]() is
is ![]() . Also, the dimensions of the other sides of the
. Also, the dimensions of the other sides of the ![]() can be
easily computed:
can be
easily computed: ![]() and
and ![]() . This allows us to compute one side of the
triangle
. This allows us to compute one side of the
triangle ![]() ,
, ![]() . Therefore, the scale factor
. Therefore, the scale factor ![]() to
to ![]() is
is ![]() , which yields the length of
, which yields the length of ![]() as
as ![]() .
Therefore, the scale factor for
.
Therefore, the scale factor for ![]() to
to ![]() is
is ![]() . Some more algebraic manipulation will show that
. Some more algebraic manipulation will show that ![]() to
to ![]() is still
is still ![]() . Also, since the triangles are disjoint, the area of the union is the sum of the areas. Therefore, the area is the geometric series
. Also, since the triangles are disjoint, the area of the union is the sum of the areas. Therefore, the area is the geometric series
![]() At this point, it may be wise to "simplify"
At this point, it may be wise to "simplify" ![]() .
So the geometric series converges to
.
So the geometric series converges to
 .
Using the diffference of squares, we get
.
Using the diffference of squares, we get ![]() , which simplifies to
, which simplifies to ![]() . Cancellling all common factors, we get the reduced fraction,
. Cancellling all common factors, we get the reduced fraction, ![]() , yielding the answer
, yielding the answer ![]() .
.
See also
| 2013 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 12 |
Followed by Problem 14 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.