Difference between revisions of "2013 AMC 10A Problems/Problem 20"
Claudeaops (talk | contribs) (Image) |
Claudeaops (talk | contribs) (Image) |
||
| Line 26: | Line 26: | ||
For this square with side length 1, the distance from center to vertex is <math>r = \frac{1}{\sqrt{2}}</math>, hence the area is composed of a semicircle of radius <math>r</math>, plus <math>4</math> times a parallelogram with height <math>\frac{1}{2}</math> and base <math>\frac{\sqrt{2}}{2(1+\sqrt{2})}</math>. That is to say, the total area is <math>\frac{1}{2} \pi (1/\sqrt{2})^2 + 4 \frac{\sqrt{2}}{4(1+\sqrt{2})} = \boxed{\textbf{(C) } \frac{\pi}{4} + 2 - \sqrt{2}}</math>. | For this square with side length 1, the distance from center to vertex is <math>r = \frac{1}{\sqrt{2}}</math>, hence the area is composed of a semicircle of radius <math>r</math>, plus <math>4</math> times a parallelogram with height <math>\frac{1}{2}</math> and base <math>\frac{\sqrt{2}}{2(1+\sqrt{2})}</math>. That is to say, the total area is <math>\frac{1}{2} \pi (1/\sqrt{2})^2 + 4 \frac{\sqrt{2}}{4(1+\sqrt{2})} = \boxed{\textbf{(C) } \frac{\pi}{4} + 2 - \sqrt{2}}</math>. | ||
| + | |||
| + | [[Image:AMC 10A 2013 -20.png]] | ||
==See Also== | ==See Also== | ||
Revision as of 01:34, 18 August 2014
Problem
A unit square is rotated ![]() about its center. What is the area of the region swept out by the interior of the square?
about its center. What is the area of the region swept out by the interior of the square?
![]()
Solution 1
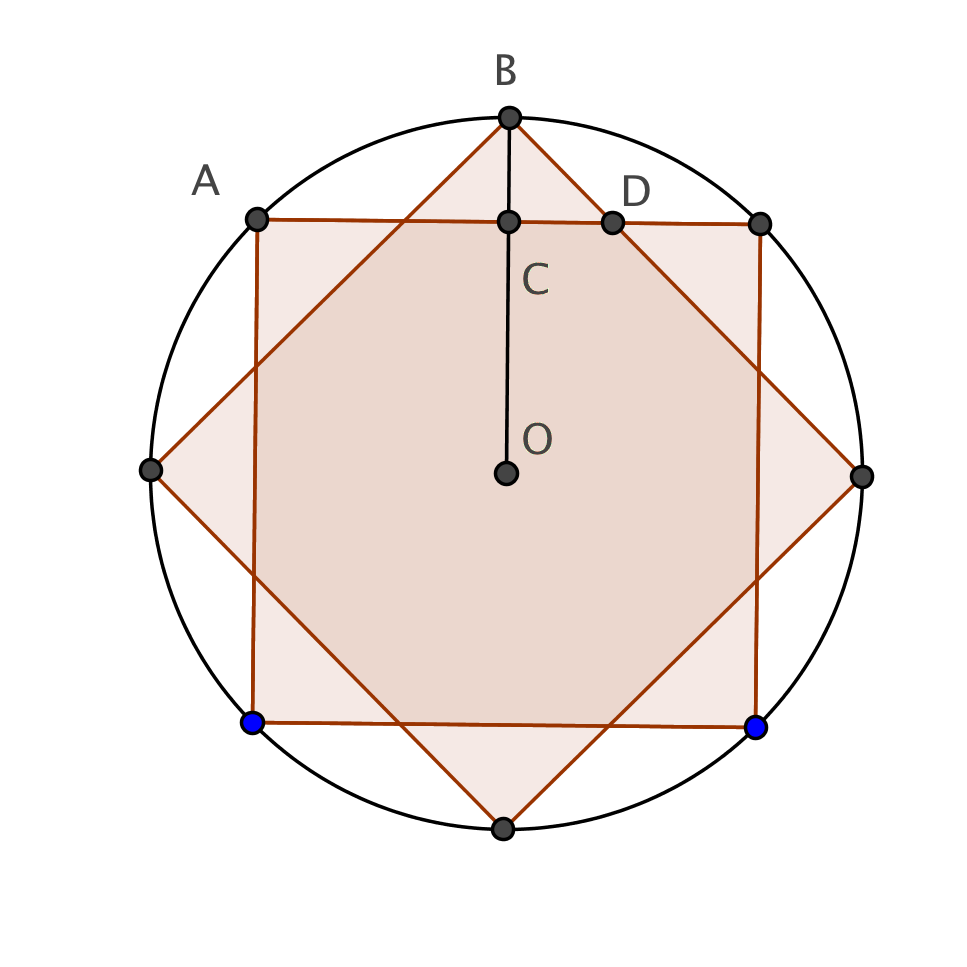
First, we need to see what this looks like. Below is a diagram.
![[asy] size(200); defaultpen(linewidth(0.8)); path square=shift((-.5,-.5))*unitsquare,square2=rotate(45)*square; fill(square^^square2,grey); for(int i=0;i<=3;i=i+1) { path arcrot=arc(origin,sqrt(2)/2,45+90*i,90*(i+1)); draw(arcrot); fill(arcrot--((sqrt(2)-1)/(2*sqrt(2)),0)--cycle,grey); draw(arc(origin,sqrt(2)/2+1/8,50+90*i,90*(i+1)-10),EndArrow); } draw(square^^square2);[/asy]](http://latex.artofproblemsolving.com/0/c/a/0caec9712738ab044db79a8329cb13fd0006a610.png)
For this square with side length 1, the distance from center to vertex is ![]() , hence the area is composed of a semicircle of radius
, hence the area is composed of a semicircle of radius ![]() , plus
, plus ![]() times a parallelogram with height
times a parallelogram with height ![]() and base
and base ![]() . That is to say, the total area is
. That is to say, the total area is ![]() .
.
See Also
| 2013 AMC 10A (Problems • Answer Key • Resources) | ||
| Preceded by Problem 19 |
Followed by Problem 21 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.