Difference between revisions of "2013 AMC 8 Problems/Problem 18"
(→Solution) |
m (→Solution 2: super minor typo) |
||
| Line 17: | Line 17: | ||
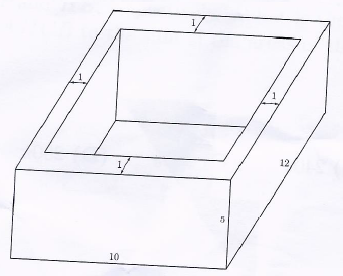
We can just calculate the volume of the prism that was cut out of the original <math>12\times 10\times 5</math> box. Each interior side of the fort will be <math>2</math> feet shorter than each side of the outside. Since the floor is <math>1</math> foot, the height will be <math>4</math> feet. So the volume of the interior box is <math>10\times 8\times 4=320\text{ ft}^3</math>. | We can just calculate the volume of the prism that was cut out of the original <math>12\times 10\times 5</math> box. Each interior side of the fort will be <math>2</math> feet shorter than each side of the outside. Since the floor is <math>1</math> foot, the height will be <math>4</math> feet. So the volume of the interior box is <math>10\times 8\times 4=320\text{ ft}^3</math>. | ||
| − | The volume of the original box is <math>12\times 10\times 5=600\text{ ft}^3</math>. Therefore, the number of | + | The volume of the original box is <math>12\times 10\times 5=600\text{ ft}^3</math>. Therefore, the number of blocks contained in the fort is <math>600-320=\boxed{\textbf{(B)}\ 280}</math>. |
==See Also== | ==See Also== | ||
{{AMC8 box|year=2013|num-b=17|num-a=19}} | {{AMC8 box|year=2013|num-b=17|num-a=19}} | ||
{{MAA Notice}} | {{MAA Notice}} | ||
Revision as of 23:43, 27 November 2013
Contents
Problem
Isabella uses one-foot cubical blocks to build a rectangular fort that is 12 feet long, 10 feet wide, and 5 feet high. The floor and the four walls are all one foot thick. How many blocks does the fort contain?
--Arpanliku 16:22, 27 November 2013 (EST) Courtesy of Lord.of.AMC
![]()
Solution 1
There are ![]() cubes on the base of the box. Then, for each of the 4 layers above the bottom (as since each cube is 1 foot by 1 foot by 1 foot and the box is 5 feet tall, there are 4 feet left), there are
cubes on the base of the box. Then, for each of the 4 layers above the bottom (as since each cube is 1 foot by 1 foot by 1 foot and the box is 5 feet tall, there are 4 feet left), there are ![]() cubes. Hence, the answer is
cubes. Hence, the answer is ![]() .
.
Solution 2
We can just calculate the volume of the prism that was cut out of the original ![]() box. Each interior side of the fort will be
box. Each interior side of the fort will be ![]() feet shorter than each side of the outside. Since the floor is
feet shorter than each side of the outside. Since the floor is ![]() foot, the height will be
foot, the height will be ![]() feet. So the volume of the interior box is
feet. So the volume of the interior box is ![]() .
.
The volume of the original box is ![]() . Therefore, the number of blocks contained in the fort is
. Therefore, the number of blocks contained in the fort is ![]() .
.
See Also
| 2013 AMC 8 (Problems • Answer Key • Resources) | ||
| Preceded by Problem 17 |
Followed by Problem 19 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AJHSME/AMC 8 Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.