2014 IMO Problems/Problem 4
Problem
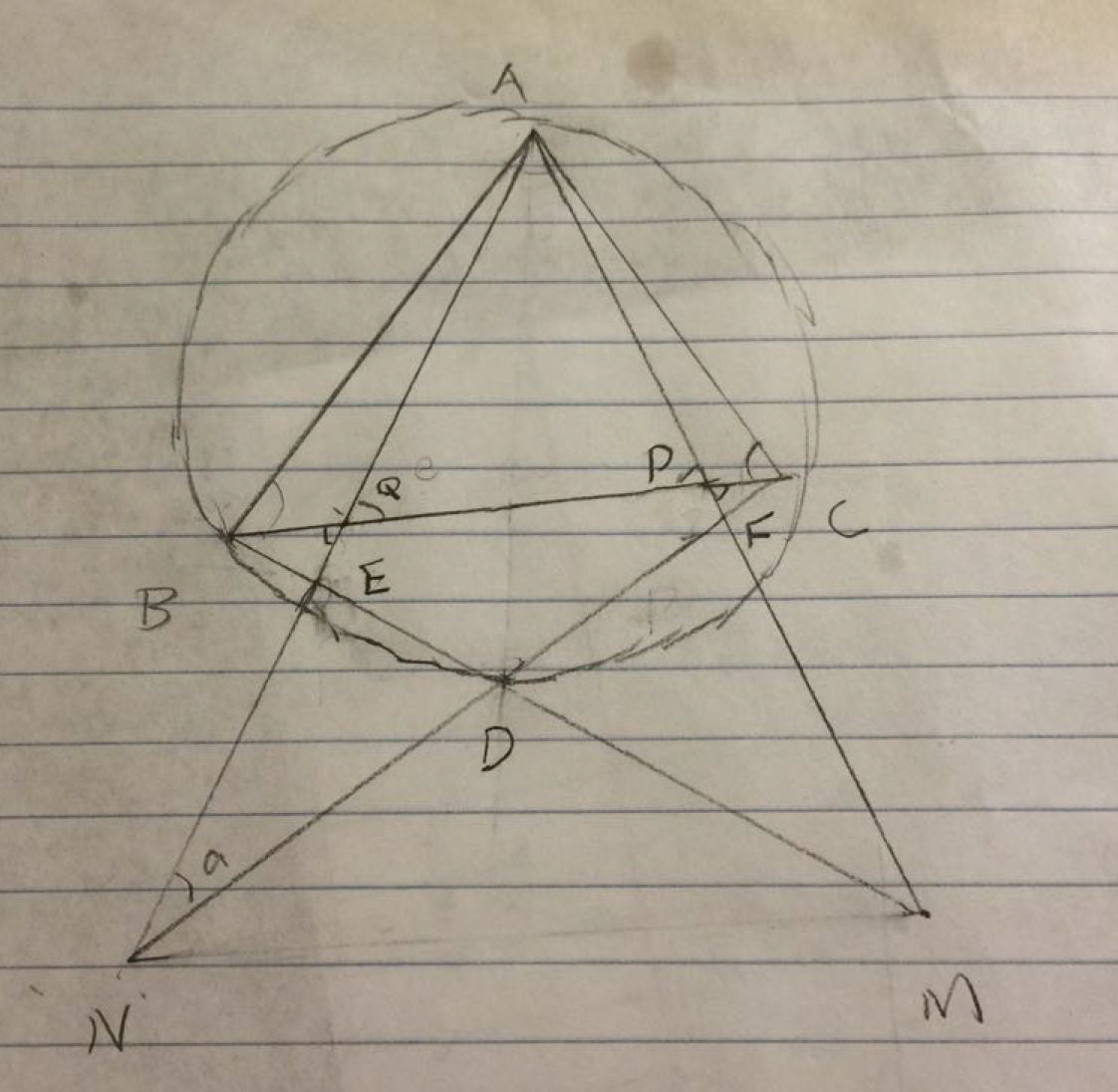
Points ![]() and
and ![]() lie on side
lie on side ![]() of acute-angled
of acute-angled ![]() so that
so that ![]() and
and ![]() . Points
. Points ![]() and
and ![]() lie on lines
lie on lines ![]() and
and ![]() , respectively, such that
, respectively, such that ![]() is the midpoint of
is the midpoint of ![]() , and
, and ![]() is the midpoint of
is the midpoint of ![]() . Prove that lines
. Prove that lines ![]() and
and ![]() intersect on the circumcircle of
intersect on the circumcircle of ![]() .
.
Solution
Sorry guys I'm new to AOPS so I don't know how to insert equations and stuff. Please help if you can. Thanks.
We are trying to prove that the intersection of BM and CN, call it point D, is on the circumcircle of triangle ABC. In other words, we are trying to prove angle BAC plus angle BDC is 180 degrees. Let the intersection of BM and AN be point E, and the intersection of AM and CN be point F. Let us assume (angle BDC) + (angle BAC) = 180. If angle BDC plus angle BAC is 180, then angle BAC should be equal to angles BDN and CDM. We can quickly prove that the triangles ABC, APB, and AQC are similar, so angles BAC = AQC = APB. We also see that angles AQC = BQN = APB = CPF. Also because angles BEQ and NED, MFD and CFP are equal, the triangles BEQ and NED, MDF and FCP must be two pairs of similar triangles. Therefore we must prove angles CBM and ANC, AMB and BCN are equal. We have angles BQA = APC = NQC = BPM. We also have AQ = QN, AP = PM. Because the triangles ABP and ACQ are similar, we have EC/EN = BF/FM, so triangles BFM and NEC are similar. So the angles CBM and ANC, BCN and AMB are equal and we are done.
Alternate solutions are always welcome. If you have a different, elegant solution to this problem, please add it to this page.
See Also
| 2014 IMO (Problems) • Resources | ||
| Preceded by Problem 3 |
1 • 2 • 3 • 4 • 5 • 6 | Followed by Problem 5 |
| All IMO Problems and Solutions | ||