Difference between revisions of "2017 AIME II Problems/Problem 15"
Expilncalc (talk | contribs) (→Solution 3) |
m (→Solution 3) |
||
| (25 intermediate revisions by 6 users not shown) | |||
| Line 1: | Line 1: | ||
==Problem== | ==Problem== | ||
| − | Tetrahedron <math>ABCD</math> has <math>AD=BC=28</math>, <math>AC=BD=44</math>, and <math>AB=CD=52</math>. For any point <math>X</math> in space, | + | Tetrahedron <math>ABCD</math> has <math>AD=BC=28</math>, <math>AC=BD=44</math>, and <math>AB=CD=52</math>. For any point <math>X</math> in space, suppose <math>f(X)=AX+BX+CX+DX</math>. The least possible value of <math>f(X)</math> can be expressed as <math>m\sqrt{n}</math>, where <math>m</math> and <math>n</math> are positive integers, and <math>n</math> is not divisible by the square of any prime. Find <math>m+n</math>. |
| − | ==Solution== | + | |
| − | + | ==Official Solution (MAA)== | |
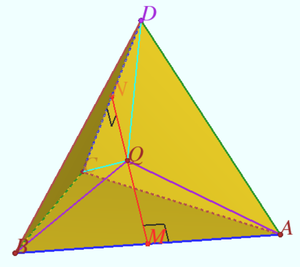
| + | [[File:2017 AIME II 15.png|300px|right]] | ||
Let <math>M</math> and <math>N</math> be midpoints of <math>\overline{AB}</math> and <math>\overline{CD}</math>. The given conditions imply that <math>\triangle ABD\cong\triangle BAC</math> and <math>\triangle CDA\cong\triangle DCB</math>, and therefore <math>MC=MD</math> and <math>NA=NB</math>. It follows that <math>M</math> and <math>N</math> both lie on the common perpendicular bisector of <math>\overline{AB}</math> and <math>\overline{CD}</math>, and thus line <math>MN</math> is that common perpendicular bisector. Points <math>B</math> and <math>C</math> are symmetric to <math>A</math> and <math>D</math> with respect to line <math>MN</math>. If <math>X</math> is a point in space and <math>X'</math> is the point symmetric to <math>X</math> with respect to line <math>MN</math>, then <math>BX=AX'</math> and <math>CX=DX'</math>, so <math>f(X) = AX+AX'+DX+DX'</math>. | Let <math>M</math> and <math>N</math> be midpoints of <math>\overline{AB}</math> and <math>\overline{CD}</math>. The given conditions imply that <math>\triangle ABD\cong\triangle BAC</math> and <math>\triangle CDA\cong\triangle DCB</math>, and therefore <math>MC=MD</math> and <math>NA=NB</math>. It follows that <math>M</math> and <math>N</math> both lie on the common perpendicular bisector of <math>\overline{AB}</math> and <math>\overline{CD}</math>, and thus line <math>MN</math> is that common perpendicular bisector. Points <math>B</math> and <math>C</math> are symmetric to <math>A</math> and <math>D</math> with respect to line <math>MN</math>. If <math>X</math> is a point in space and <math>X'</math> is the point symmetric to <math>X</math> with respect to line <math>MN</math>, then <math>BX=AX'</math> and <math>CX=DX'</math>, so <math>f(X) = AX+AX'+DX+DX'</math>. | ||
Let <math>Q</math> be the intersection of <math>\overline{XX'}</math> and <math>\overline{MN}</math>. Then <math>AX+AX'\geq 2AQ</math>, from which it follows that <math>f(X) \geq 2(AQ+DQ) = f(Q)</math>. It remains to minimize <math>f(Q)</math> as <math>Q</math> moves along <math>\overline{MN}</math>. | Let <math>Q</math> be the intersection of <math>\overline{XX'}</math> and <math>\overline{MN}</math>. Then <math>AX+AX'\geq 2AQ</math>, from which it follows that <math>f(X) \geq 2(AQ+DQ) = f(Q)</math>. It remains to minimize <math>f(Q)</math> as <math>Q</math> moves along <math>\overline{MN}</math>. | ||
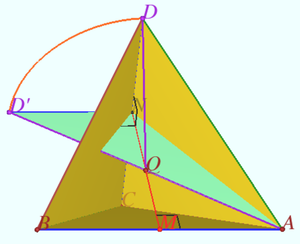
| − | + | [[File:2017 AIME II 15a.png|300px|right]] | |
Allow <math>D</math> to rotate about <math>\overline{MN}</math> to point <math>D'</math> in the plane <math>AMN</math> on the side of <math>\overline{MN}</math> opposite <math>A</math>. Because <math>\angle DNM</math> is a right angle, <math>D'N=DN</math>. It then follows that <math>f(Q) = 2(AQ+D'Q)\geq 2AD'</math>, and equality occurs when <math>Q</math> is the intersection of <math>\overline{AD'}</math> and <math>\overline{MN}</math>. Thus <math>\min f(Q) = 2AD'</math>. Because <math>\overline{MD}</math> is the median of <math>\triangle ADB</math>, the Length of Median Formula shows that <math>4MD^2 = 2AD^2 + 2BD^2 - AB^2 = 2\cdot 28^2 + 2 \cdot 44^2 - 52^2</math> and <math>MD^2 = 684</math>. By the Pythagorean Theorem <math>MN^2 = MD^2 - ND^2 = 8</math>. | Allow <math>D</math> to rotate about <math>\overline{MN}</math> to point <math>D'</math> in the plane <math>AMN</math> on the side of <math>\overline{MN}</math> opposite <math>A</math>. Because <math>\angle DNM</math> is a right angle, <math>D'N=DN</math>. It then follows that <math>f(Q) = 2(AQ+D'Q)\geq 2AD'</math>, and equality occurs when <math>Q</math> is the intersection of <math>\overline{AD'}</math> and <math>\overline{MN}</math>. Thus <math>\min f(Q) = 2AD'</math>. Because <math>\overline{MD}</math> is the median of <math>\triangle ADB</math>, the Length of Median Formula shows that <math>4MD^2 = 2AD^2 + 2BD^2 - AB^2 = 2\cdot 28^2 + 2 \cdot 44^2 - 52^2</math> and <math>MD^2 = 684</math>. By the Pythagorean Theorem <math>MN^2 = MD^2 - ND^2 = 8</math>. | ||
Because <math>\angle AMN</math> and <math>\angle D'NM</math> are right angles, <cmath>(AD')^2 = (AM+D'N)^2 + MN^2 = (2AM)^2 + MN^2 = 52^2 + 8 = 4\cdot 678.</cmath>It follows that <math>\min f(Q) = 2AD' = 4\sqrt{678}</math>. The requested sum is <math>4+678=\boxed{682}</math>. | Because <math>\angle AMN</math> and <math>\angle D'NM</math> are right angles, <cmath>(AD')^2 = (AM+D'N)^2 + MN^2 = (2AM)^2 + MN^2 = 52^2 + 8 = 4\cdot 678.</cmath>It follows that <math>\min f(Q) = 2AD' = 4\sqrt{678}</math>. The requested sum is <math>4+678=\boxed{682}</math>. | ||
| − | + | ==Solution 2== | |
Set <math>a=BC=28</math>, <math>b=CA=44</math>, <math>c=AB=52</math>. Let <math>O</math> be the point which minimizes <math>f(X)</math>. | Set <math>a=BC=28</math>, <math>b=CA=44</math>, <math>c=AB=52</math>. Let <math>O</math> be the point which minimizes <math>f(X)</math>. | ||
| − | + | <math>\boxed{\textrm{Claim 1: } O \textrm{ is the gravity center } \ \tfrac {1}{4}(\vec A + \vec B + \vec C + \vec D)}</math> | |
| − | Proof | + | |
| + | <math>\textrm{Proof:}</math> Let <math>M</math> and <math>N</math> denote the midpoints of <math>AB</math> and <math>CD</math>. From <math>\triangle ABD \cong \triangle BAC</math> and <math>\triangle CDA \cong \triangle DCB</math>, we have <math>MC=MD</math>, <math>NA=NB</math> an hence <math>MN</math> is a perpendicular bisector of both segments <math>AB</math> and <math>CD</math>. Then if <math>X</math> is any point inside tetrahedron <math>ABCD</math>, its orthogonal projection onto line <math>MN</math> will have smaller <math>f</math>-value; hence we conclude that <math>O</math> must lie on <math>MN</math>. Similarly, <math>O</math> must lie on the line joining the midpoints of <math>AC</math> and <math>BD</math>. <math>\square</math> | ||
| + | |||
| + | <math>\boxed{\textrm{Claim 2: The gravity center } O \textrm{ coincides with the circumcenter.} \phantom{\vec A}}</math> | ||
| − | + | <math>\textrm{Proof:}</math> Let <math>G_D</math> be the centroid of triangle <math>ABC</math>; then <math>DO = \tfrac 34 DG_D</math> (by vectors). If we define <math>G_A</math>, <math>G_B</math>, <math>G_C</math> similarly, we get <math>AO = \tfrac 34 AG_A</math> and so on. But from symmetry we have <math>AG_A = BG_B = CG_C = DG_D</math>, hence <math>AO = BO = CO = DO</math>. <math>\square</math> | |
| − | |||
| − | Now we use the fact that an isosceles tetrahedron has circumradius <math>R = \sqrt{\ | + | Now we use the fact that an isosceles tetrahedron has circumradius <math>R = \sqrt{\tfrac18(a^2+b^2+c^2)}</math>. |
| − | + | Here <math>R = \sqrt{678}</math> so <math>f(O) = 4R = 4\sqrt{678}</math>. Therefore, the answer is <math>4 + 678 = \boxed{682}</math>. | |
| − | |||
| − | + | ==Solution 3== | |
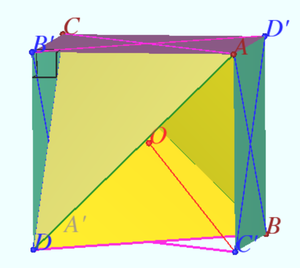
| − | < | + | [[File:2017 AIME II 15b.png|300px|right]] |
| − | + | Isosceles tetrahedron <math>ABCD</math> or [https://en.wikipedia.org/wiki/Disphenoid Disphenoid] can be inscribed in a parallelepiped <math>AB'CD'C'DA'B,</math> whose facial diagonals are the pares of equal edges of the tetrahedron <math>(AC = B'D',</math> where <math>B'D' = BD).</math> This parallelepiped is right-angled, therefore it is circumscribed and has equal diagonals. The center O of the circumscribed sphere (coincide with the centroid) has equal distance from each vertex. Tetrachedrons <math>ABCD</math> and <math>A'B'C'D'</math> are congruent, so point of symmetry O is point of minimum <math>f(X). f(O)= 4R</math>, where <math>R</math> is the circumradius of parallelepiped. | |
| − | + | <cmath>8R^2 = 2 CC'^2 = 2CD'^2 + 2D'B^2 + 2BC'^2, </cmath> | |
| + | <cmath>2 CC'^2 = (CD'^2 + BC'^2) + (BC'^2 + BD'^2) + (CD'^2 + BD'^2) = AC^2 + AB^2+BC^2,</cmath> | ||
| + | <cmath>R = OC =\sqrt{\frac {AB^2 + AC^2 + AD^2}{8}}, f(O)= 4R = 4\sqrt {678}.</cmath> | ||
| − | + | '''vladimir.shelomovskii@gmail.com, vvsss''' (Reconstruction) | |
| − | |||
| − | =See Also= | + | ==See Also== |
{{AIME box|year=2017|n=II|num-b=14|after=Last Question}} | {{AIME box|year=2017|n=II|num-b=14|after=Last Question}} | ||
| + | [[Category:Intermediate Geometry Problems]] | ||
| + | [[Category:3D Geometry Problems]] | ||
{{MAA Notice}} | {{MAA Notice}} | ||
Latest revision as of 02:08, 22 January 2024
Problem
Tetrahedron ![]() has
has ![]() ,
, ![]() , and
, and ![]() . For any point
. For any point ![]() in space, suppose
in space, suppose ![]() . The least possible value of
. The least possible value of ![]() can be expressed as
can be expressed as ![]() , where
, where ![]() and
and ![]() are positive integers, and
are positive integers, and ![]() is not divisible by the square of any prime. Find
is not divisible by the square of any prime. Find ![]() .
.
Official Solution (MAA)
Let ![]() and
and ![]() be midpoints of
be midpoints of ![]() and
and ![]() . The given conditions imply that
. The given conditions imply that ![]() and
and ![]() , and therefore
, and therefore ![]() and
and ![]() . It follows that
. It follows that ![]() and
and ![]() both lie on the common perpendicular bisector of
both lie on the common perpendicular bisector of ![]() and
and ![]() , and thus line
, and thus line ![]() is that common perpendicular bisector. Points
is that common perpendicular bisector. Points ![]() and
and ![]() are symmetric to
are symmetric to ![]() and
and ![]() with respect to line
with respect to line ![]() . If
. If ![]() is a point in space and
is a point in space and ![]() is the point symmetric to
is the point symmetric to ![]() with respect to line
with respect to line ![]() , then
, then ![]() and
and ![]() , so
, so ![]() .
.
Let ![]() be the intersection of
be the intersection of ![]() and
and ![]() . Then
. Then ![]() , from which it follows that
, from which it follows that ![]() . It remains to minimize
. It remains to minimize ![]() as
as ![]() moves along
moves along ![]() .
.
Allow ![]() to rotate about
to rotate about ![]() to point
to point ![]() in the plane
in the plane ![]() on the side of
on the side of ![]() opposite
opposite ![]() . Because
. Because ![]() is a right angle,
is a right angle, ![]() . It then follows that
. It then follows that ![]() , and equality occurs when
, and equality occurs when ![]() is the intersection of
is the intersection of ![]() and
and ![]() . Thus
. Thus ![]() . Because
. Because ![]() is the median of
is the median of ![]() , the Length of Median Formula shows that
, the Length of Median Formula shows that ![]() and
and ![]() . By the Pythagorean Theorem
. By the Pythagorean Theorem ![]() .
.
Because ![]() and
and ![]() are right angles,
are right angles, ![]() It follows that
It follows that ![]() . The requested sum is
. The requested sum is ![]() .
.
Solution 2
Set ![]() ,
, ![]() ,
, ![]() . Let
. Let ![]() be the point which minimizes
be the point which minimizes ![]() .
.
![]()
![]() Let
Let ![]() and
and ![]() denote the midpoints of
denote the midpoints of ![]() and
and ![]() . From
. From ![]() and
and ![]() , we have
, we have ![]() ,
, ![]() an hence
an hence ![]() is a perpendicular bisector of both segments
is a perpendicular bisector of both segments ![]() and
and ![]() . Then if
. Then if ![]() is any point inside tetrahedron
is any point inside tetrahedron ![]() , its orthogonal projection onto line
, its orthogonal projection onto line ![]() will have smaller
will have smaller ![]() -value; hence we conclude that
-value; hence we conclude that ![]() must lie on
must lie on ![]() . Similarly,
. Similarly, ![]() must lie on the line joining the midpoints of
must lie on the line joining the midpoints of ![]() and
and ![]() .
. ![]()
![]()
![]() Let
Let ![]() be the centroid of triangle
be the centroid of triangle ![]() ; then
; then ![]() (by vectors). If we define
(by vectors). If we define ![]() ,
, ![]() ,
, ![]() similarly, we get
similarly, we get ![]() and so on. But from symmetry we have
and so on. But from symmetry we have ![]() , hence
, hence ![]() .
. ![]()
Now we use the fact that an isosceles tetrahedron has circumradius ![]() .
.
Here ![]() so
so ![]() . Therefore, the answer is
. Therefore, the answer is ![]() .
.
Solution 3
Isosceles tetrahedron ![]() or Disphenoid can be inscribed in a parallelepiped
or Disphenoid can be inscribed in a parallelepiped ![]() whose facial diagonals are the pares of equal edges of the tetrahedron
whose facial diagonals are the pares of equal edges of the tetrahedron ![]() where
where ![]() This parallelepiped is right-angled, therefore it is circumscribed and has equal diagonals. The center O of the circumscribed sphere (coincide with the centroid) has equal distance from each vertex. Tetrachedrons
This parallelepiped is right-angled, therefore it is circumscribed and has equal diagonals. The center O of the circumscribed sphere (coincide with the centroid) has equal distance from each vertex. Tetrachedrons ![]() and
and ![]() are congruent, so point of symmetry O is point of minimum
are congruent, so point of symmetry O is point of minimum ![]() , where
, where ![]() is the circumradius of parallelepiped.
is the circumradius of parallelepiped.
![]()
![]()
![]()
vladimir.shelomovskii@gmail.com, vvsss (Reconstruction)
See Also
| 2017 AIME II (Problems • Answer Key • Resources) | ||
| Preceded by Problem 14 |
Followed by Last Question | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.