Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2017 IMO Problems/Problem 4"
(→‎Solution)
Line 2: Line 2:
  
 
==Solution==
 
==Solution==
 +
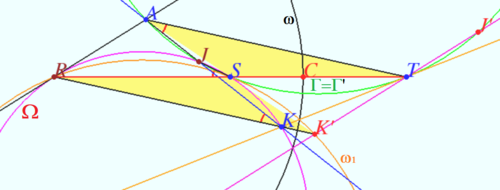
[[File:2017 IMO 4.png|500px|right]]
 
We construct inversion which maps <math>KT</math> into the circle <math>\omega_1</math> and  <math>\Gamma</math> into  <math>\Gamma.</math> Than we prove that <math>\omega_1</math> is tangent to <math>\Gamma.</math>
 
We construct inversion which maps <math>KT</math> into the circle <math>\omega_1</math> and  <math>\Gamma</math> into  <math>\Gamma.</math> Than we prove that <math>\omega_1</math> is tangent to <math>\Gamma.</math>
  
 
Quadrungle <math>RJSK</math> is cyclic <math>\implies \angle RSJ = \angle RKJ.</math>
 
Quadrungle <math>RJSK</math> is cyclic <math>\implies \angle RSJ = \angle RKJ.</math>
 
Quadrungle <math>AJST</math> is cyclic <math>\implies \angle RSJ = \angle TAJ \implies AT||RK.</math>
 
Quadrungle <math>AJST</math> is cyclic <math>\implies \angle RSJ = \angle TAJ \implies AT||RK.</math>
−
We construct circle <math>\omega</math> centered at <math>R</math> which maps  <math>\Gamma</math> into  <math>\Gamma.</math> Let <math>C = \omega \cap RT \implies RC^2 = RS \cdot RT.</math> Inversion with respect <math>\omega</math> swap <math>T</math> and <math>S \implies  \Gamma</math> maps into  <math>\Gamma.</math>
+
 
 +
We construct circle <math>\omega</math> centered at <math>R</math> which maps  <math>\Gamma</math> into  <math>\Gamma.</math> Let <math>C = \omega \cap RT \implies RC^2 = RS \cdot RT.</math> Inversion with respect <math>\omega</math> swap <math>T</math> and <math>S \implies  \Gamma</math> maps into  <math>\Gamma (\Gamma = \Gamma').</math> Let <math>O</math> be the center of <math>\Gamma.</math>
 +
 
 
Inversion with respect <math>\omega</math>  maps <math>K</math> into <math>K'</math>.
 
Inversion with respect <math>\omega</math>  maps <math>K</math> into <math>K'</math>.
 +
<math>K</math> belong <math>KT \implies</math> circle  <math>K'SR</math> is the image of <math>KT</math>. Let <math>Q</math> be the center of the circle  <math>K'SR.</math>
 +
 +
<math>K'T</math> is the image of <math>\Omega</math> at this inversion, <math>l = AR</math> is tangent line to <math>\Omega</math> at <math>R,</math> so <math>K'T||AR.</math>
 +
 +
<math>K'</math> is image K at this inversion <math>\implies K \in RK' \implies RK'||AT \implies ARK'T</math> is parallelogramm.
 +
 +
<math>S</math> is the midpoint of <math>RT \implies S</math> is the center of symmetry of <math>ATK'R \implies</math>
 +
<math>\triangle RSK'</math> is symmetrical to <math>\triangle TSA</math> with respect to <math>S \implies</math>
 +
circumcircle <math>RSK'</math>  is symmetrical to circumcircle <math>TSA</math> with respect to <math>S \implies</math>
 +
<math>O</math> is symmetrycal <math>Q</math> with respect to <math>S, S</math> lies on <math>\Gamma</math> and on <math>|omega_1 \implies</math>
 +
<math>\Gamma</math> is tangent <math>\omega_1 \implies S\Gamma</math> is tangent <math>\omega_1.</math>

Revision as of 12:01, 26 August 2022

Let $R$ and $S$ be different points on a circle $\Omega$ such that $RS$ is not a diameter. Let $\ell$ be the tangent line to $\Omega$ at $R$. Point $T$ is such that $S$ is the midpoint of the line segment $RT$. Point $J$ is chosen on the shorter arc $RS$ of $\Omega$ so that the circumcircle $\Gamma$ of triangle $JST$ intersects $\ell$ at two distinct points. Let $A$ be the common point of $\Gamma$ and $\ell$ that is closer to $R$. Line $AJ$ meets $\Omega$ again at $K$. Prove that the line $KT$ is tangent to $\Gamma$.

Solution

2017 IMO 4.png

We construct inversion which maps $KT$ into the circle $\omega_1$ and $\Gamma$ into $\Gamma.$ Than we prove that $\omega_1$ is tangent to $\Gamma.$

Quadrungle $RJSK$ is cyclic $\implies \angle RSJ = \angle RKJ.$ Quadrungle $AJST$ is cyclic $\implies \angle RSJ = \angle TAJ \implies AT||RK.$

We construct circle $\omega$ centered at $R$ which maps $\Gamma$ into $\Gamma.$ Let $C = \omega \cap RT \implies RC^2 = RS \cdot RT.$ Inversion with respect $\omega$ swap $T$ and $S \implies \Gamma$ maps into $\Gamma (\Gamma = \Gamma').$ Let $O$ be the center of $\Gamma.$

Inversion with respect $\omega$ maps $K$ into $K'$. $K$ belong $KT \implies$ circle $K'SR$ is the image of $KT$. Let $Q$ be the center of the circle $K'SR.$

$K'T$ is the image of $\Omega$ at this inversion, $l = AR$ is tangent line to $\Omega$ at $R,$ so $K'T||AR.$

$K'$ is image K at this inversion $\implies K \in RK' \implies RK'||AT \implies ARK'T$ is parallelogramm.

$S$ is the midpoint of $RT \implies S$ is the center of symmetry of $ATK'R \implies$ $\triangle RSK'$ is symmetrical to $\triangle TSA$ with respect to $S \implies$ circumcircle $RSK'$ is symmetrical to circumcircle $TSA$ with respect to $S \implies$ $O$ is symmetrycal $Q$ with respect to $S, S$ lies on $\Gamma$ and on $|omega_1 \implies$ $\Gamma$ is tangent $\omega_1 \implies S\Gamma$ is tangent $\omega_1.$

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2017_IMO_Problems/Problem_4&oldid=177512"