Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2017 IMO Problems/Problem 4"

(→‎Solution)
(→‎Solution)
Line 29: Line 29:
  
 
'''vladimir.shelomovskii@gmail.com, vvsss'''
 
'''vladimir.shelomovskii@gmail.com, vvsss'''
 +
 +
==Solution 2==
 +
[[File:2017 IMO 4a.png|500px|right]]
 +
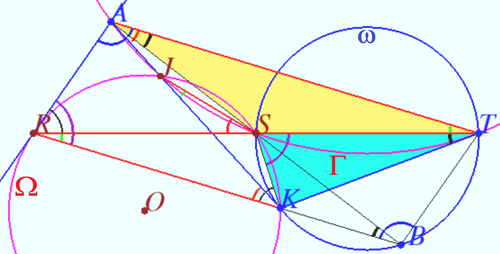
We use the equality of the inscribed angle and the angle between the chord and the tangent to prove that a line is a tangent.
 +
 +
Quadrungle <math>RJSK</math> is cyclic <math>\implies \angle RSJ = \angle RKJ.</math>
 +
Quadrungle <math>AJST</math> is cyclic <math>\implies \angle RSJ = \angle TAJ \implies AT||RK.</math>
 +
Let <math>B</math> be symmetric to <math>A</math> with respect to <math>S \implies ATBR</math> is parallelogram.
 +
<math>\angle KST = \angle SAK + \angle SKR = \angle KRA</math>
 +
<math>\angle RBT = \angle RAT \implies \angle KST + \angle KBT = 180^\circ \implies SKBT</math> is cyclic.
 +
<math>\angle SBK = \angle STK  = \angle SAT \implies </math>
 +
Inscribed angle of <math>\Gamma \angle SAT</math> is equal to angle between KT and chord ST \implies <math>KT</math> is tangent to <math>\Gamma.</math>

Revision as of 15:25, 26 August 2022

Let $R$ and $S$ be different points on a circle $\Omega$ such that $RS$ is not a diameter. Let $\ell$ be the tangent line to $\Omega$ at $R$. Point $T$ is such that $S$ is the midpoint of the line segment $RT$. Point $J$ is chosen on the shorter arc $RS$ of $\Omega$ so that the circumcircle $\Gamma$ of triangle $JST$ intersects $\ell$ at two distinct points. Let $A$ be the common point of $\Gamma$ and $\ell$ that is closer to $R$. Line $AJ$ meets $\Omega$ again at $K$. Prove that the line $KT$ is tangent to $\Gamma$.

Solution

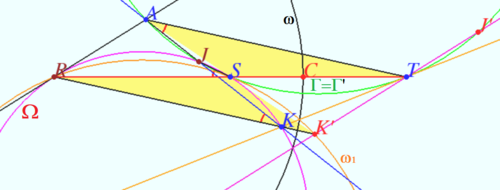
2017 IMO 4.png

We construct inversion which maps $KT$ into the circle $\omega_1$ and $\Gamma$ into $\Gamma.$ Than we prove that $\omega_1$ is tangent to $\Gamma.$

Quadrungle $RJSK$ is cyclic $\implies \angle RSJ = \angle RKJ.$ Quadrungle $AJST$ is cyclic $\implies \angle RSJ = \angle TAJ \implies AT||RK.$

We construct circle $\omega$ centered at $R$ which maps $\Gamma$ into $\Gamma.$

Let $C = \omega \cap RT \implies RC^2 = RS \cdot RT.$ Inversion with respect $\omega$ swap $T$ and $S \implies \Gamma$ maps into $\Gamma (\Gamma = \Gamma').$

Let $O$ be the center of $\Gamma.$

Inversion with respect $\omega$ maps $K$ into $K'$. $K$ belong $KT \implies$ circle $K'SR = \omega_1$ is the image of $KT$. Let $Q$ be the center of $\omega_1.$

$K'T$ is the image of $\Omega$ at this inversion, $l = AR$ is tangent line to $\Omega$ at $R,$ so $K'T||AR.$

$K'$ is image K at this inversion $\implies K \in RK' \implies RK'||AT \implies ARK'T$ is parallelogram.

$S$ is the midpoint of $RT \implies S$ is the center of symmetry of $ATK'R \implies$ $\triangle RSK'$ is symmetrical to $\triangle TSA$ with respect to $S \implies$ $\omega_1$ is symmetrical to $\Gamma$ with respect to $S \implies$ $O$ is symmetrycal $Q$ with respect to $S.$

$S$ lies on $\Gamma$ and on $\omega_1 \implies \Gamma$ is tangent to $\omega_1 \implies$ line $KT$ is tangent to $\Gamma.$

vladimir.shelomovskii@gmail.com, vvsss

Solution 2

2017 IMO 4a.png

We use the equality of the inscribed angle and the angle between the chord and the tangent to prove that a line is a tangent.

Quadrungle $RJSK$ is cyclic $\implies \angle RSJ = \angle RKJ.$ Quadrungle $AJST$ is cyclic $\implies \angle RSJ = \angle TAJ \implies AT||RK.$ Let $B$ be symmetric to $A$ with respect to $S \implies ATBR$ is parallelogram. $\angle KST = \angle SAK + \angle SKR = \angle KRA$ $\angle RBT = \angle RAT \implies \angle KST + \angle KBT = 180^\circ \implies SKBT$ is cyclic. $\angle SBK = \angle STK = \angle SAT \implies$ Inscribed angle of $\Gamma \angle SAT$ is equal to angle between KT and chord ST \implies $KT$ is tangent to $\Gamma.$

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2017_IMO_Problems/Problem_4&oldid=177538"