Difference between revisions of "2018 AMC 10B Problems/Problem 10"
m (→Problem) |
Swaglikeohio (talk | contribs) m (→Solution 1) |
||
| (30 intermediate revisions by 8 users not shown) | |||
| Line 46: | Line 46: | ||
==Solution 1== | ==Solution 1== | ||
| − | Consider the cross-sectional plane and label its area <math>b</math>. Note that the volume of the triangular prism that encloses the pyramid is <math>\frac{bh}{2}=3</math>, and we want the rectangular pyramid that shares the base and height with the triangular prism. The volume of the pyramid is <math>\frac{bh}{3}</math>, so the answer is <math>\boxed{2}</math>. (AOPS12142015) | + | Consider the cross-sectional plane and label its area <math>b</math>. Note that the volume of the triangular prism that encloses the pyramid is <math>\frac{bh}{2}=3</math>, and we want the rectangular pyramid that shares the base and height with the triangular prism. The volume of the pyramid is <math>\frac{bh}{3}</math>, so the answer is <math>\boxed{(E) 2}</math>.uwu (AOPS12142015) |
==Solution 2== | ==Solution 2== | ||
We can start by finding the total volume of the parallelepiped. It is <math>2 \cdot 3 \cdot 1 = 6</math>, because a rectangular parallelepiped is a rectangular prism. | We can start by finding the total volume of the parallelepiped. It is <math>2 \cdot 3 \cdot 1 = 6</math>, because a rectangular parallelepiped is a rectangular prism. | ||
| − | Next, we can consider the wedge-shaped section made when the plane <math>BCHE</math> cuts the figure. We can find the volume of the triangular pyramid with base EFB and apex M. The area of EFB is <math>\frac{1}{2} \cdot 2 \cdot 3 = 3</math>. Since BC is given to be <math>1</math>, we have that FM is <math>\frac{1}{2}</math>. Using the formula for the volume of a triangular pyramid, we have <math>V = \frac{1}{3} \cdot \frac{1}{2} \cdot 3 = \frac{1}{2}</math>. Also, since the triangular pyramid with base HGC and apex M has the exact same dimensions, it has volume <math>\frac{1}{2}</math> as well. | + | Next, we can consider the wedge-shaped section made when the plane <math>BCHE</math> cuts the figure. We can find the volume of the triangular pyramid with base <math>EFB</math> and apex <math>M</math>. The area of <math>EFB</math> is <math>\frac{1}{2} \cdot 2 \cdot 3 = 3</math>. Since <math>\overline{BC}</math> is given to be <math>1</math>, we have that <math>\overline{FM}</math> is <math>\frac{1}{2}</math>. Using the formula for the volume of a triangular pyramid, we have <math>V = \frac{1}{3} \cdot \frac{1}{2} \cdot 3 = \frac{1}{2}</math>. Also, since the triangular pyramid with base <math>HGC</math> and apex <math>M</math> has the exact same dimensions, it has volume <math>\frac{1}{2}</math> as well. |
The original wedge we considered in the last step has volume <math>3</math>, because it is half of the volume of the parallelepiped. We can subtract out the parts we found to have <math>3 - \frac{1}{2} \cdot 2 = 2</math>. Thus, the volume of the figure we are trying to find is <math>2</math>. This means that the correct answer choice is <math>\boxed{E}</math>. | The original wedge we considered in the last step has volume <math>3</math>, because it is half of the volume of the parallelepiped. We can subtract out the parts we found to have <math>3 - \frac{1}{2} \cdot 2 = 2</math>. Thus, the volume of the figure we are trying to find is <math>2</math>. This means that the correct answer choice is <math>\boxed{E}</math>. | ||
| Line 62: | Line 62: | ||
If you look carefully, you will see that on the either side of the pyramid in question, there are two congruent tetrahedra. The volume of one is <math>\frac{1}{3}Bh</math>, with its base being half of one of the rectangular prism's faces and its height being half of one of the edges, so its volume is <math>\frac{1}{3} (3 \times 2/2 \times \frac{1}{2})=\frac{1}{2}</math>. We can obtain the answer by subtracting twice this value from the diagonal half prism, or | If you look carefully, you will see that on the either side of the pyramid in question, there are two congruent tetrahedra. The volume of one is <math>\frac{1}{3}Bh</math>, with its base being half of one of the rectangular prism's faces and its height being half of one of the edges, so its volume is <math>\frac{1}{3} (3 \times 2/2 \times \frac{1}{2})=\frac{1}{2}</math>. We can obtain the answer by subtracting twice this value from the diagonal half prism, or | ||
<math>(\frac{1}{2} \times 3 \times 2 \times 1) - (2 \times \frac{1}{2})= </math> <math>\boxed{2}</math> | <math>(\frac{1}{2} \times 3 \times 2 \times 1) - (2 \times \frac{1}{2})= </math> <math>\boxed{2}</math> | ||
| + | |||
| + | ==Solution 4== | ||
| + | You can calculate the volume of the rectangular pyramid by using the formula, <math>\frac{Ah}{3}</math>. <math>A</math> is the area of the base, <math>BCHE</math>, and is equal to <math>BC * BE</math>. The height, <math>h</math>, is equal to the height of triangle <math>FBE</math> drawn from <math>F</math> to <math>BE</math>. | ||
| + | |||
| + | <math>BE=\sqrt{BF^2 + EF^2}=\sqrt{13}</math> Area of <math>BCHE = BC * BE = \sqrt{13}</math> | ||
| + | |||
| + | <math>h = 2 *</math> Area of <math>FBE / BE</math> (since Area <math>= \frac{1}{2}bh</math>). | ||
| + | |||
| + | Area of <math>FBE = \frac{1}{2} * FB * FE = 3</math> | ||
| + | |||
| + | <math>h = 2 * 3 / \sqrt{13} = \frac{6}{\sqrt{13}}</math> | ||
| + | |||
| + | Volume of pyramid <math>=\frac{1}{3} * \sqrt{13} * \frac{6}{\sqrt{13}} = 2</math> | ||
| + | |||
| + | Answer is <math>\boxed{\textbf{E } 2}</math> | ||
| + | |||
| + | ~OlutosinNGA | ||
| + | |||
| + | == Solution 5 == | ||
| + | We can start by identifying the information we need. We need to find the area of rectangle <math>EHCB</math> and the height of rectangular prism <math>EHCBM</math>. | ||
| + | |||
| + | In order to find the area of <math>EHCB,</math> we can use the Pythagorean Theorem. We find that <math>EB = \sqrt{13}</math>, so the area of rectangle <math>EHCB = \sqrt{13}</math>. We shall refer to this as <math>x</math>. | ||
| + | |||
| + | In order to find the height of rectangular prism <math>EHCBM</math>, we can examine triangle <math>EFB</math>. We can use the Geometric Mean Theorem to find that when an altitude is dropped from point <math>F,</math> <math>\overline{EB}</math> is split into segments of length <math>\dfrac{4 \cdot \sqrt{13}}{13}</math> and <math>\dfrac{9 \cdot \sqrt{13}}{13}</math>. Taking the geometric mean of these numbers, we find that the altitude has length <math>\dfrac{6 \cdot \sqrt{13}}{13}</math>. This is also the height of the rectangular prism, which we shall refer to as <math>y</math>. | ||
| + | |||
| + | Plugging <math>x</math> and <math>y</math> into the formula <math>V = \dfrac{b \cdot h}{3},</math> we find that the volume is <math>\boxed{2}</math>. The answer is <math>\boxed{E}</math>. | ||
| + | |||
| + | == Solution 6 == | ||
| + | We start by setting the formula for the volume of a rectangular pyramid: <math>\frac{1}{3}Bh</math>. By the Pythagorean Theorem, we know that <math>BE = \sqrt{BF^2 + EF^2} = \sqrt{13}</math>. Therefore, the area of the base is <math>1 \times \sqrt{13} = \sqrt{13}</math>. Next, we would like to know the height of the pyramid. We can observe that the altitude from point <math>F</math> in <math>\triangle EFB</math> is parallel to the height of the pyramid and therefore congruent because those two altitudes are on the same plane of base <math>EBCH</math>. From this, we only need to find the altitude from point <math>F</math> in <math>\triangle EFB</math> and plug it into our formula for the volume of a rectangular pyramid. This is easy because we already know the area of <math>\triangle EFB</math> and the base from point <math>F</math>, so all we need to do is divide: <math>\frac{2 \times 3}{\sqrt{13}} = \frac{6}{\sqrt{13}} = \frac{6\sqrt{13}}{13}</math>. Now all we need to do is plug in all our known values into the volume formula: <math>\frac{1}{3}Bh = \frac{\sqrt{13} \times \frac{6\sqrt{13}}{13}}{3} = \boxed{(E) 2}</math> | ||
| + | |||
| + | ~ellpet | ||
| + | |||
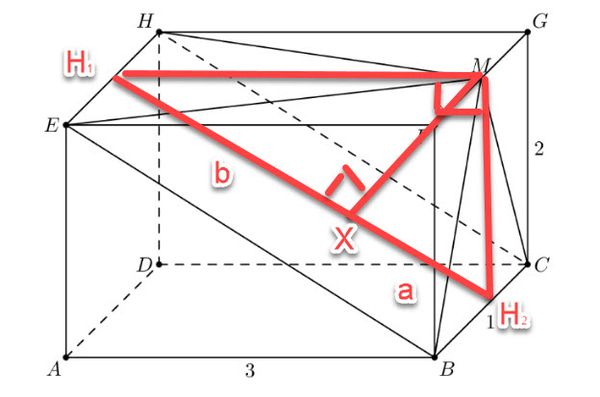
| + | == Solution 7 == | ||
| + | |||
| + | [[File:AMC 10B 10 2018.jpg|600px]] | ||
| + | |||
| + | Using the Pythagorean Theorem, we can easily find that <math>EB = \sqrt{2^2 + 3^2} = \sqrt{13}</math>. Quickly computing, we find the area of the base, <math>BCHE = \sqrt{13} \cdot 1 = \sqrt{13}</math>. Now we can make the following adjustments to our 3d shape as shown in the diagram. All we need now is to solve for the height, or <math>XM</math>. We can set up to following equation due to our knowledge of altitudes(of the hypotenuse)in right triangles. We can set up the following equations: | ||
| + | <cmath>\begin{align*} | ||
| + | b(a+b) &= (MH_1)^2 \\ | ||
| + | a(a+b) &= (MH_2)^2 \\ | ||
| + | b\sqrt{13} &= 3^2 \\ | ||
| + | a\sqrt{13} &= 2^2 \\ | ||
| + | b &= \dfrac{9}{\sqrt{13}} \\ | ||
| + | a &= \dfrac{4}{\sqrt{13}} \\ | ||
| + | (MX)^2 &= ab \\ | ||
| + | (MX)^2 &= \dfrac{9 \cdot 4}{13} \\ | ||
| + | MX &= \dfrac {3 \cdot 2}{\sqrt{13}} \\ | ||
| + | \end{align*}</cmath> | ||
| + | Thus <math>\triangle V_{BCHEM} = \dfrac{\text{(height)}\cdot \text{(base)}}{3} = \dfrac{MX \cdot BCHE}{3} = \dfrac {\sqrt{13} \cdot \dfrac{3 \cdot 2}{\sqrt{13}}}{3}</math> <math>= \boxed{\textbf{(E) } 2}</math> | ||
| + | |||
| + | ~ Wiselion :) | ||
| + | |||
| + | ==Video Solution (HOW TO THINK CREATIVELY)== | ||
| + | https://youtu.be/tlbbP_NdPmc | ||
| + | |||
| + | ~Education, the Study of Everything | ||
==See Also== | ==See Also== | ||
Latest revision as of 01:13, 16 January 2024
Contents
Problem
In the rectangular parallelepiped shown, ![]() =
= ![]() ,
, ![]() =
= ![]() , and
, and ![]() =
= ![]() . Point
. Point ![]() is the midpoint of
is the midpoint of ![]() . What is the volume of the rectangular pyramid with base
. What is the volume of the rectangular pyramid with base ![]() and apex
and apex ![]() ?
?
![[asy] size(250); defaultpen(fontsize(10pt)); pair A =origin; pair B = (4.75,0); pair E1=(0,3); pair F = (4.75,3); pair G = (5.95,4.2); pair C = (5.95,1.2); pair D = (1.2,1.2); pair H= (1.2,4.2); pair M = ((4.75+5.95)/2,3.6); draw(E1--M--H--E1--A--B--E1--F--B--M--C--G--H); draw(B--C); draw(F--G); draw(A--D--H--C--D,dashed); label("$A$",A,SW); label("$B$",B,SE); label("$C$",C,E); label("$D$",D,W); label("$E$",E1,W); label("$F$",F,SW); label("$G$",G,NE); label("$H$",H,NW); label("$M$",M,N); dot(A); dot(B); dot(E1); dot(F); dot(G); dot(C); dot(D); dot(H); dot(M); label("3",A/2+B/2,S); label("2",C/2+G/2,E); label("1",C/2+B/2,SE); [/asy]](http://latex.artofproblemsolving.com/8/8/5/885c4e50ebdac89dd6aba698666a62eaa1b5eba6.png)
![]()
Solution 1
Consider the cross-sectional plane and label its area ![]() . Note that the volume of the triangular prism that encloses the pyramid is
. Note that the volume of the triangular prism that encloses the pyramid is ![]() , and we want the rectangular pyramid that shares the base and height with the triangular prism. The volume of the pyramid is
, and we want the rectangular pyramid that shares the base and height with the triangular prism. The volume of the pyramid is ![]() , so the answer is
, so the answer is ![]() .uwu (AOPS12142015)
.uwu (AOPS12142015)
Solution 2
We can start by finding the total volume of the parallelepiped. It is ![]() , because a rectangular parallelepiped is a rectangular prism.
, because a rectangular parallelepiped is a rectangular prism.
Next, we can consider the wedge-shaped section made when the plane ![]() cuts the figure. We can find the volume of the triangular pyramid with base
cuts the figure. We can find the volume of the triangular pyramid with base ![]() and apex
and apex ![]() . The area of
. The area of ![]() is
is ![]() . Since
. Since ![]() is given to be
is given to be ![]() , we have that
, we have that ![]() is
is ![]() . Using the formula for the volume of a triangular pyramid, we have
. Using the formula for the volume of a triangular pyramid, we have ![]() . Also, since the triangular pyramid with base
. Also, since the triangular pyramid with base ![]() and apex
and apex ![]() has the exact same dimensions, it has volume
has the exact same dimensions, it has volume ![]() as well.
as well.
The original wedge we considered in the last step has volume ![]() , because it is half of the volume of the parallelepiped. We can subtract out the parts we found to have
, because it is half of the volume of the parallelepiped. We can subtract out the parts we found to have ![]() . Thus, the volume of the figure we are trying to find is
. Thus, the volume of the figure we are trying to find is ![]() . This means that the correct answer choice is
. This means that the correct answer choice is ![]() .
.
Written by: Archimedes15
NOTE: For those who think that it isn't a rectangular prism, please read the problem. It says "rectangular parallelepiped." If a parallelepiped is such that all of the faces are rectangles, it is a rectangular prism.
Solution 3
If you look carefully, you will see that on the either side of the pyramid in question, there are two congruent tetrahedra. The volume of one is ![]() , with its base being half of one of the rectangular prism's faces and its height being half of one of the edges, so its volume is
, with its base being half of one of the rectangular prism's faces and its height being half of one of the edges, so its volume is ![]() . We can obtain the answer by subtracting twice this value from the diagonal half prism, or
. We can obtain the answer by subtracting twice this value from the diagonal half prism, or
![]()
![]()
Solution 4
You can calculate the volume of the rectangular pyramid by using the formula, ![]() .
. ![]() is the area of the base,
is the area of the base, ![]() , and is equal to
, and is equal to ![]() . The height,
. The height, ![]() , is equal to the height of triangle
, is equal to the height of triangle ![]() drawn from
drawn from ![]() to
to ![]() .
.
![]() Area of
Area of ![]()
![]() Area of
Area of ![]() (since Area
(since Area ![]() ).
).
Area of ![]()
![]()
Volume of pyramid ![]()
Answer is ![]()
~OlutosinNGA
Solution 5
We can start by identifying the information we need. We need to find the area of rectangle ![]() and the height of rectangular prism
and the height of rectangular prism ![]() .
.
In order to find the area of ![]() we can use the Pythagorean Theorem. We find that
we can use the Pythagorean Theorem. We find that ![]() , so the area of rectangle
, so the area of rectangle ![]() . We shall refer to this as
. We shall refer to this as ![]() .
.
In order to find the height of rectangular prism ![]() , we can examine triangle
, we can examine triangle ![]() . We can use the Geometric Mean Theorem to find that when an altitude is dropped from point
. We can use the Geometric Mean Theorem to find that when an altitude is dropped from point ![]()
![]() is split into segments of length
is split into segments of length ![]() and
and ![]() . Taking the geometric mean of these numbers, we find that the altitude has length
. Taking the geometric mean of these numbers, we find that the altitude has length ![]() . This is also the height of the rectangular prism, which we shall refer to as
. This is also the height of the rectangular prism, which we shall refer to as ![]() .
.
Plugging ![]() and
and ![]() into the formula
into the formula ![]() we find that the volume is
we find that the volume is ![]() . The answer is
. The answer is ![]() .
.
Solution 6
We start by setting the formula for the volume of a rectangular pyramid: ![]() . By the Pythagorean Theorem, we know that
. By the Pythagorean Theorem, we know that ![]() . Therefore, the area of the base is
. Therefore, the area of the base is ![]() . Next, we would like to know the height of the pyramid. We can observe that the altitude from point
. Next, we would like to know the height of the pyramid. We can observe that the altitude from point ![]() in
in ![]() is parallel to the height of the pyramid and therefore congruent because those two altitudes are on the same plane of base
is parallel to the height of the pyramid and therefore congruent because those two altitudes are on the same plane of base ![]() . From this, we only need to find the altitude from point
. From this, we only need to find the altitude from point ![]() in
in ![]() and plug it into our formula for the volume of a rectangular pyramid. This is easy because we already know the area of
and plug it into our formula for the volume of a rectangular pyramid. This is easy because we already know the area of ![]() and the base from point
and the base from point ![]() , so all we need to do is divide:
, so all we need to do is divide: ![]() . Now all we need to do is plug in all our known values into the volume formula:
. Now all we need to do is plug in all our known values into the volume formula: ![]()
~ellpet
Solution 7
Using the Pythagorean Theorem, we can easily find that ![]() . Quickly computing, we find the area of the base,
. Quickly computing, we find the area of the base, ![]() . Now we can make the following adjustments to our 3d shape as shown in the diagram. All we need now is to solve for the height, or
. Now we can make the following adjustments to our 3d shape as shown in the diagram. All we need now is to solve for the height, or ![]() . We can set up to following equation due to our knowledge of altitudes(of the hypotenuse)in right triangles. We can set up the following equations:
. We can set up to following equation due to our knowledge of altitudes(of the hypotenuse)in right triangles. We can set up the following equations:
 Thus
Thus 
![]()
~ Wiselion :)
Video Solution (HOW TO THINK CREATIVELY)
~Education, the Study of Everything
See Also
| 2018 AMC 10B (Problems • Answer Key • Resources) | ||
| Preceded by Problem 9 |
Followed by Problem 11 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.