2019 AMC 10B Problems/Problem 22
- The following problem is from both the 2019 AMC 10B #22 and 2019 AMC 12B #19, so both problems redirect to this page.
Contents
Problem
Raashan, Sylvia, and Ted play the following game. Each starts with ![]() . A bell rings every
. A bell rings every ![]() seconds, at which time each of the players who currently have money simultaneously chooses one of the other two players independently and at random and gives
seconds, at which time each of the players who currently have money simultaneously chooses one of the other two players independently and at random and gives ![]() to that player. What is the probability that after the bell has rung
to that player. What is the probability that after the bell has rung ![]() times, each player will have
times, each player will have ![]() ? (For example, Raashan and Ted may each decide to give
? (For example, Raashan and Ted may each decide to give ![]() to Sylvia, and Sylvia may decide to give her dollar to Ted, at which point Raashan will have
to Sylvia, and Sylvia may decide to give her dollar to Ted, at which point Raashan will have ![]() , Sylvia will have
, Sylvia will have ![]() , and Ted will have
, and Ted will have ![]() , and that is the end of the first round of play. In the second round Rashaan has no money to give, but Sylvia and Ted might choose each other to give their
, and that is the end of the first round of play. In the second round Rashaan has no money to give, but Sylvia and Ted might choose each other to give their ![]() to, and the holdings will be the same at the end of the second round.)
to, and the holdings will be the same at the end of the second round.)
![]()
Solution 1
On the first turn, each player starts off with ![]() . Each turn after that, there are only two possibilities: either everyone stays at
. Each turn after that, there are only two possibilities: either everyone stays at ![]() , which we will write as
, which we will write as ![]() , or the distribution of money becomes
, or the distribution of money becomes ![]() in some order, which we write as
in some order, which we write as ![]() . (
. (![]() cannot be achieved since either(1)the person cannot give money to himself or (2)there are a maximum of 2 dollars being distributed and the person has nothing to start with). We will consider these two states separately.
cannot be achieved since either(1)the person cannot give money to himself or (2)there are a maximum of 2 dollars being distributed and the person has nothing to start with). We will consider these two states separately.
In the ![]() state, each person has two choices for whom to give their dollar to, meaning there are
state, each person has two choices for whom to give their dollar to, meaning there are ![]() possible ways that the money can be rearranged. Note that there are only two ways that we can reach
possible ways that the money can be rearranged. Note that there are only two ways that we can reach ![]() again:
again:
1. Raashan gives his money to Sylvia, who gives her money to Ted, who gives his money to Raashan.
2. Raashan gives his money to Ted, who gives his money to Sylvia, who gives her money to Raashan.
Thus, the probability of staying in the ![]() state is
state is ![]() , while the probability of going to the
, while the probability of going to the ![]() state is
state is ![]() (we can check that the 6 other possibilities lead to
(we can check that the 6 other possibilities lead to ![]() )
)
In the ![]() state, we will label the person with
state, we will label the person with ![]() as person A, the person with
as person A, the person with ![]() as person B, and the person with
as person B, and the person with ![]() as person C. Person A has two options for whom to give money to, and person B has 2 options for whom to give money to, meaning there are total
as person C. Person A has two options for whom to give money to, and person B has 2 options for whom to give money to, meaning there are total ![]() ways the money can be redistributed. The only way that the distribution can return to
ways the money can be redistributed. The only way that the distribution can return to ![]() is if A gives
is if A gives ![]() to B, and B gives
to B, and B gives ![]() to C. We check the other possibilities to find that they all lead back to
to C. We check the other possibilities to find that they all lead back to ![]() . Thus, the probability of going to the
. Thus, the probability of going to the ![]() state is
state is ![]() , while the probability of staying in the
, while the probability of staying in the ![]() state is
state is ![]() .
.
No matter which state we are in, the probability of going to the ![]() state is always
state is always ![]() . This means that, after the bell rings 2018 times, regardless of what state the money distribution is in, there is a
. This means that, after the bell rings 2018 times, regardless of what state the money distribution is in, there is a ![]() probability of going to the
probability of going to the ![]() state after the 2019th bell ring. Thus, our answer is simply
state after the 2019th bell ring. Thus, our answer is simply ![]() .
.
Solution 2 (Symmetry)
After the first ring, either nothing changes, or someone has ![]() . No one can have
. No one can have ![]() , since in that hypothetical round, that person would have to give away
, since in that hypothetical round, that person would have to give away ![]() . Thus, the outcome is either
. Thus, the outcome is either ![]() or six symmetrical cases where one person gets
or six symmetrical cases where one person gets ![]() (e.g. a
(e.g. a ![]() or
or ![]() split).
split).
Case 1: Probability of returning to 1-1-1 from 1-1-1
There are two ways for the three people to exchange dollars to get to the same ![]() result. To see this, seat R, S, and T in a circle. Each person gives their dollar to either the person at left, or at right, to result in again 1 dollar for each person. There are 8 overall possibilities (since each person has 2 choices when giving away his or her dollar, therefore
result. To see this, seat R, S, and T in a circle. Each person gives their dollar to either the person at left, or at right, to result in again 1 dollar for each person. There are 8 overall possibilities (since each person has 2 choices when giving away his or her dollar, therefore ![]() total possibilities). So, there is
total possibilities). So, there is ![]() chance of returning to
chance of returning to ![]() .
.
Case 2: Probability of returning to 1-1-1 from 2-1-0
Without loss of generality, take the ![]() case. Only 2 people can give money, so there are now
case. Only 2 people can give money, so there are now ![]() possible outcomes after the bell rings. It either decomposes back into
possible outcomes after the bell rings. It either decomposes back into ![]() ,
, ![]() (remained unchanged),
(remained unchanged), ![]() ,
, ![]() . Thus, there is a
. Thus, there is a ![]() chance of returning to
chance of returning to ![]() . Notice that this works for any of the 6 cases, as each is symmetrical to the others.
. Notice that this works for any of the 6 cases, as each is symmetrical to the others.
Answer
Since the starting state has a ![]() chance of remaining unchanged, and each of the different 6 symmetric states all also have a
chance of remaining unchanged, and each of the different 6 symmetric states all also have a ![]() chance of reverting back to
chance of reverting back to ![]() , the chance of it being
, the chance of it being ![]() after any state is always
after any state is always ![]() .
.
Solution 3
The two possible scenarios are they all have ![]() dollar, or one person has
dollar, or one person has ![]() dollars, another has
dollars, another has ![]() , and the last has none. We will consider the second scenario all to be the same no matter who has the
, and the last has none. We will consider the second scenario all to be the same no matter who has the ![]() dollars,
dollars, ![]() dollar or
dollar or ![]() dollars from symmetry.
dollars from symmetry.
Let's consider all possible scenarios when the bell rings if they currently all have 1 dollar.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() We see that
We see that ![]() or
or ![]() of the cases lead to them continuing to all of them having
of the cases lead to them continuing to all of them having ![]() dollar.
Now, let's consider all the possible scenarios when the bell rings if they currently have
dollar.
Now, let's consider all the possible scenarios when the bell rings if they currently have ![]() dollars. Without loss of generality, let's say that R and S have
dollars. Without loss of generality, let's say that R and S have ![]() and
and ![]() dollar respectively. (We can switch the names, our answer won't change).
dollar respectively. (We can switch the names, our answer won't change).
![]()
![]()
![]()
![]() We see that
We see that ![]() of the cases lead to them changing to all have
of the cases lead to them changing to all have ![]() dollar.
dollar.
So, no matter what was the scenario when the bell had been rung ![]() times, when the bell is rung the
times, when the bell is rung the ![]() th time, there is always a
th time, there is always a ![]() chance that it will turn into (or stay as)
chance that it will turn into (or stay as) ![]()
Solution 4 (Markov Chain)
Let the state ![]() be
be ![]() , and state
, and state ![]() without considering the order be
without considering the order be ![]() . Similar to the previous
. Similar to the previous ![]() solutions, after a bell ring, the probability of state
solutions, after a bell ring, the probability of state ![]() staying in state
staying in state ![]() is
is ![]() , that of state
, that of state ![]() transiting to state
transiting to state ![]() is
is ![]() , that of state
, that of state ![]() staying in state
staying in state ![]() is
is ![]() , that of state
, that of state ![]() transiting to state
transiting to state ![]() is
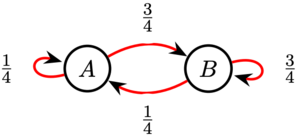
is ![]() . Using Markov Chain, the state transition diagram is shown below.
. Using Markov Chain, the state transition diagram is shown below.

![]() and
and ![]() are equivalent, from
are equivalent, from ![]() or
or ![]() , we get
, we get ![]() . Solving the system of equations, we get
. Solving the system of equations, we get ![]()
Note: the number of bell rings doesn't matter, ![]() is redundant.
is redundant.
Solution 5 (Risky Guessing)
This works if one is short on time. Looking at how simple answer choices are, it seems like the number of bell rings is extra information (the other solutions show that this is true). So, we assume that the probability will be the same no matter how many times the bell rings, and we calculate it for ![]() bell ring. Each person can give their dollar to
bell ring. Each person can give their dollar to ![]() other people, so there are
other people, so there are ![]() ways to switch up the money. Out of these
ways to switch up the money. Out of these ![]() ways,
ways, ![]() of them leave everyone with a dollar again, so our probability is
of them leave everyone with a dollar again, so our probability is ![]() .
.
Video Solution by OmegaLearn
https://youtu.be/rLAcJe3o-uA?t=1086
~ pi_is_3.14
Video Solution
See Also
| 2019 AMC 10B (Problems • Answer Key • Resources) | ||
| Preceded by Problem 21 |
Followed by Problem 23 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
| 2019 AMC 12B (Problems • Answer Key • Resources) | |
| Preceded by Problem 18 |
Followed by Problem 20 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.