Difference between revisions of "2019 AMC 10B Problems/Problem 23"
Sevenoptimus (talk | contribs) m (Fixed a typo in Solution 3) |
Isabelchen (talk | contribs) |
||
| (40 intermediate revisions by 20 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{duplicate|[[2019 AMC 10B Problems|2019 AMC 10B #23]] and [[2019 AMC 12B Problems|2019 AMC 12B #20]]}} | + | {{duplicate|[[2019 AMC 10B Problems#Problem 23|2019 AMC 10B #23]] and [[2019 AMC 12B Problems#Problem 20|2019 AMC 12B #20]]}} |
==Problem== | ==Problem== | ||
| − | Points <math>A(6,13)</math> and <math>B(12,11)</math> lie on circle <math>\omega</math> in the plane. Suppose that the tangent lines to <math>\omega</math> at <math>A</math> and <math>B</math> intersect at a point on the <math>x</math>-axis. What is the area of <math>\omega</math>? | + | Points <math>A=(6,13)</math> and <math>B=(12,11)</math> lie on circle <math>\omega</math> in the plane. Suppose that the tangent lines to <math>\omega</math> at <math>A</math> and <math>B</math> intersect at a point on the <math>x</math>-axis. What is the area of <math>\omega</math>? |
<math>\textbf{(A) }\frac{83\pi}{8}\qquad\textbf{(B) }\frac{21\pi}{2}\qquad\textbf{(C) } | <math>\textbf{(A) }\frac{83\pi}{8}\qquad\textbf{(B) }\frac{21\pi}{2}\qquad\textbf{(C) } | ||
| Line 9: | Line 9: | ||
==Solution 1== | ==Solution 1== | ||
| − | First, observe that the two tangent lines are of identical length. Therefore, supposing that the point of intersection is <math>(x, 0)</math>, the Pythagorean Theorem gives <math>x=5</math>. | + | First, observe that the two tangent lines are of identical length. Therefore, supposing that the point of intersection is <math>(x, 0)</math>, the Pythagorean Theorem gives <math>\sqrt{(x-6)^2 + 13^2} = \sqrt{(x-12)^2 + 11^2}</math>. This simplifies to <math>x = 5</math>. |
| − | Further, notice (due to the right angles formed by a radius and its tangent line) that the quadrilateral (a kite) | + | Further, notice (due to the right angles formed by a radius and its tangent line) that the quadrilateral (a kite) <math>AOBX</math> is cyclic. |
| − | |||
| − | ==Solution 2== | + | Therefore, we can apply [[Ptolemy's Theorem]] to give: |
| + | |||
| + | <math>2\sqrt{170}r = d \sqrt{40}</math>, where <math>r</math> is the radius of the circle and <math>d</math> is the distance between the circle's center and <math>(5, 0)</math>. Therefore, <math>d = \sqrt{17}r</math>. | ||
| + | |||
| + | Using the Pythagorean Theorem on the right triangle <math>OAX</math> (or <math>OBX</math>), we find that <math>170 + r^2 = 17r^2</math>, so <math>r^2 = \frac{85}{8}</math>, and thus the area of the circle is <math>\boxed{\textbf{(C) }\frac{85}{8}\pi}</math>. | ||
| + | |||
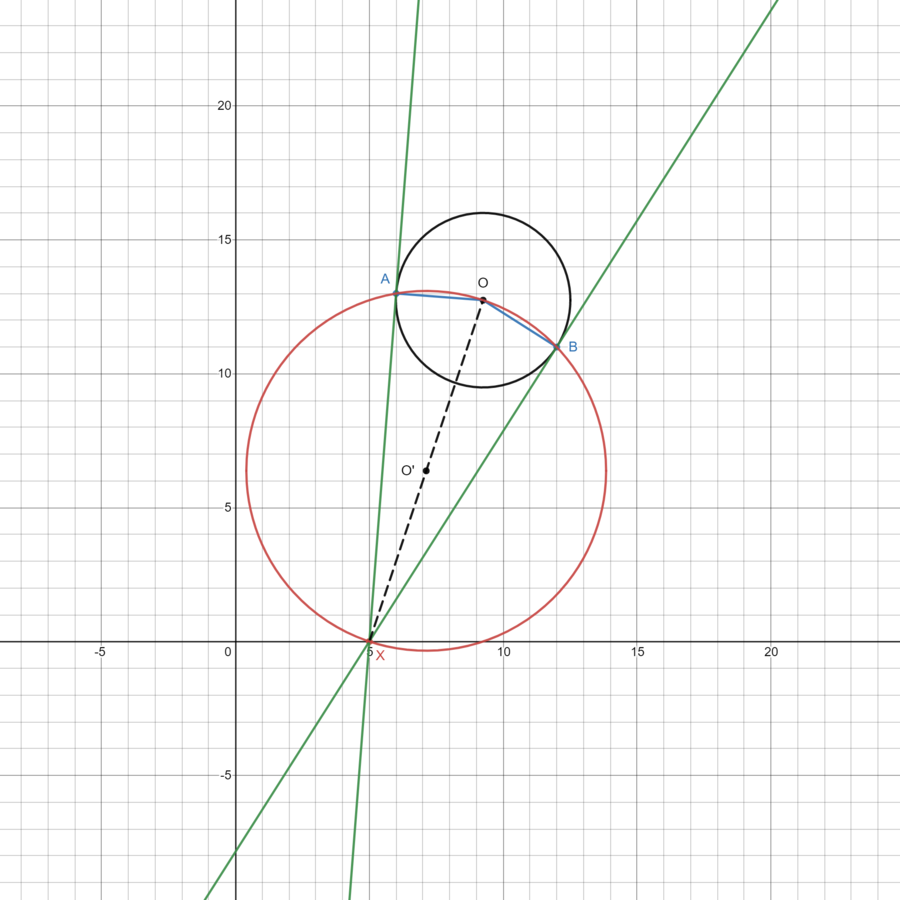
| + | ===Diagram for Solution 1=== | ||
| + | [[File:Desmos-graph (1).png|900px|caption]] | ||
| + | |||
| + | ~BakedPotato66 | ||
| + | |||
| + | ==Solution 2 (coordinate bash)== | ||
We firstly obtain <math>x=5</math> as in Solution 1. Label the point <math>(5,0)</math> as <math>C</math>. The midpoint <math>M</math> of segment <math>AB</math> is <math>(9, 12)</math>. Notice that the center of the circle must lie on the line passing through the points <math>C</math> and <math>M</math>. Thus, the center of the circle lies on the line <math>y=3x-15</math>. | We firstly obtain <math>x=5</math> as in Solution 1. Label the point <math>(5,0)</math> as <math>C</math>. The midpoint <math>M</math> of segment <math>AB</math> is <math>(9, 12)</math>. Notice that the center of the circle must lie on the line passing through the points <math>C</math> and <math>M</math>. Thus, the center of the circle lies on the line <math>y=3x-15</math>. | ||
| Line 33: | Line 43: | ||
Therefore <math>OA = \frac{AC\cdot AD}{DC}=\sqrt{\frac{85}{8}}</math>, | Therefore <math>OA = \frac{AC\cdot AD}{DC}=\sqrt{\frac{85}{8}}</math>, | ||
and consequently, the area of the circle is <math>\pi\cdot OA^2 = \boxed{\textbf{(C) }\frac{85}{8}\pi}</math>. | and consequently, the area of the circle is <math>\pi\cdot OA^2 = \boxed{\textbf{(C) }\frac{85}{8}\pi}</math>. | ||
| + | |||
| + | |||
| + | ==Solution 4 (how fast can you multiply two-digit numbers?)== | ||
| + | Let <math>(x,0)</math> be the intersection on the x-axis. By Power of a Point Theorem, <math>(x-6)^2+13^2=(x-12)^2+11^2\implies x=5</math>. Then the equations for the tangent lines passing <math>A</math> and <math>B</math>, respectively, are <math>13(x-6)+13=y</math> and <math>\frac{11}{7}(x-12)+11=y</math>. Then the lines normal (perpendicular) to them are <math>-\frac{1}{13}(x-6)+13=y</math> and <math>-\frac{7}{11}(x-12)+11=y</math>. Solving for <math>x</math>, we have | ||
| + | |||
| + | |||
| + | |||
| + | <cmath>-\frac{7}{11}(x-12)+11=-\frac{1}{13}(x-6)+13</cmath> | ||
| + | <cmath>\frac{13\cdot7x-11x}{13\cdot11}=\frac{84\cdot13-6\cdot11-2\cdot11\cdot13}{11\cdot13}</cmath> | ||
| + | <cmath>13\cdot7x-11x=84\cdot13-6\cdot11-2\cdot11\cdot13</cmath> | ||
| + | |||
| + | After condensing, <math>x=\frac{37}{4}</math>. Then, the center of <math>\omega</math> is <math>\left(\frac{37}{4}, \frac{51}{4}\right)</math>. Apply distance formula. WLOG, assume you use <math>A</math>. Then, the area of <math>\omega</math> is <cmath>\left(\sqrt{\frac{1^2}{4^2}+\frac{13^2}{4^2}}\right)^2\pi=\frac{170\pi}{16} \implies \boxed{\textbf{(C) }\frac{85}{8}\pi}.</cmath> | ||
| + | |||
| + | ==Solution 5 (tangent cheese)== | ||
| + | After getting <math>x=5</math>, let <math>C=(5,0)</math>. Get the slopes of the lines <math>AC</math> and <math>BC</math>, namely <math>\frac{13}{6-5}=13</math>, <math>\frac{11}{12-5}=\frac{11}{7}</math>. Then, use tangent angle subtraction to get <math>\tan{2x}=\frac{13-\frac{11}{7}}{1+13*\frac{11}{7}}=\frac{80}{150}=\frac{8}{15}</math>. Then, apply tangent double angle to get <math>\tan{2x}=\frac{8}{15}=\frac{2\tan{x}}{1-\tan^2{x}}</math>. Solving, we obtain <math>\tan{x}=\frac{1}{4}</math>. Then, note that <math>\tan{x}=r/{BC}</math>, so <math>r=\frac{1}{4}*\sqrt{170}</math>. Finishing off, we obtain <math>A=\pi*r^2=\pi*170/16=\boxed{\textbf{(C) }\frac{85}{8}\pi}</math>. | ||
| + | |||
| + | ~SigmaPiE | ||
| + | |||
| + | ==Video Solution== | ||
| + | For those who want a video solution: (Is similar to Solution 1) | ||
| + | https://youtu.be/WI2NVuIp1Ik | ||
| + | |||
| + | ==Video Solution by TheBeautyofMath== | ||
| + | https://youtu.be/W1zuqrTlBtU | ||
| + | |||
| + | ~IceMatrix | ||
| + | ==Video Solution by The Power of Logic== | ||
| + | https://www.youtube.com/watch?v=sQIWSrio_Hc | ||
| + | |||
| + | ~The Power of Logic | ||
==See Also== | ==See Also== | ||
Latest revision as of 10:25, 20 December 2023
- The following problem is from both the 2019 AMC 10B #23 and 2019 AMC 12B #20, so both problems redirect to this page.
Contents
[hide]Problem
Points ![]() and
and ![]() lie on circle
lie on circle ![]() in the plane. Suppose that the tangent lines to
in the plane. Suppose that the tangent lines to ![]() at
at ![]() and
and ![]() intersect at a point on the
intersect at a point on the ![]() -axis. What is the area of
-axis. What is the area of ![]() ?
?
![]()
Solution 1
First, observe that the two tangent lines are of identical length. Therefore, supposing that the point of intersection is ![]() , the Pythagorean Theorem gives
, the Pythagorean Theorem gives ![]() . This simplifies to
. This simplifies to ![]() .
.
Further, notice (due to the right angles formed by a radius and its tangent line) that the quadrilateral (a kite) ![]() is cyclic.
is cyclic.
Therefore, we can apply Ptolemy's Theorem to give:
![]() , where
, where ![]() is the radius of the circle and
is the radius of the circle and ![]() is the distance between the circle's center and
is the distance between the circle's center and ![]() . Therefore,
. Therefore, ![]() .
.
Using the Pythagorean Theorem on the right triangle ![]() (or
(or ![]() ), we find that
), we find that ![]() , so
, so ![]() , and thus the area of the circle is
, and thus the area of the circle is ![]() .
.
Diagram for Solution 1
~BakedPotato66
Solution 2 (coordinate bash)
We firstly obtain ![]() as in Solution 1. Label the point
as in Solution 1. Label the point ![]() as
as ![]() . The midpoint
. The midpoint ![]() of segment
of segment ![]() is
is ![]() . Notice that the center of the circle must lie on the line passing through the points
. Notice that the center of the circle must lie on the line passing through the points ![]() and
and ![]() . Thus, the center of the circle lies on the line
. Thus, the center of the circle lies on the line ![]() .
.
Line ![]() is
is ![]() . Therefore, the slope of the line perpendicular to
. Therefore, the slope of the line perpendicular to ![]() is
is ![]() , so its equation is
, so its equation is ![]() .
.
But notice that this line must pass through ![]() and
and ![]() . Hence
. Hence ![]() . So the center of the circle is
. So the center of the circle is ![]() .
.
Finally, the distance between the center, ![]() , and point
, and point ![]() is
is ![]() . Thus the area of the circle is
. Thus the area of the circle is ![]() .
.
Solution 3
The midpoint of ![]() is
is ![]() . Let the tangent lines at
. Let the tangent lines at ![]() and
and ![]() intersect at
intersect at ![]() on the
on the ![]() -axis. Then
-axis. Then ![]() is the perpendicular bisector of
is the perpendicular bisector of ![]() . Let the center of the circle be
. Let the center of the circle be ![]() . Then
. Then ![]() is similar to
is similar to ![]() , so
, so ![]() .
The slope of
.
The slope of ![]() is
is ![]() , so the slope of
, so the slope of ![]() is
is ![]() . Hence, the equation of
. Hence, the equation of ![]() is
is ![]() . Letting
. Letting ![]() , we have
, we have ![]() , so
, so ![]() .
.
Now, we compute ![]() ,
,
![]() , and
, and
![]() .
.
Therefore ![]() ,
and consequently, the area of the circle is
,
and consequently, the area of the circle is ![]() .
.
Solution 4 (how fast can you multiply two-digit numbers?)
Let ![]() be the intersection on the x-axis. By Power of a Point Theorem,
be the intersection on the x-axis. By Power of a Point Theorem, ![]() . Then the equations for the tangent lines passing
. Then the equations for the tangent lines passing ![]() and
and ![]() , respectively, are
, respectively, are ![]() and
and ![]() . Then the lines normal (perpendicular) to them are
. Then the lines normal (perpendicular) to them are ![]() and
and ![]() . Solving for
. Solving for ![]() , we have
, we have
![]()
![]()
![]()
After condensing, ![]() . Then, the center of
. Then, the center of ![]() is
is ![]() . Apply distance formula. WLOG, assume you use
. Apply distance formula. WLOG, assume you use ![]() . Then, the area of
. Then, the area of ![]() is
is ![\[\left(\sqrt{\frac{1^2}{4^2}+\frac{13^2}{4^2}}\right)^2\pi=\frac{170\pi}{16} \implies \boxed{\textbf{(C) }\frac{85}{8}\pi}.\]](http://latex.artofproblemsolving.com/4/c/4/4c42ef66d5323c30e0d632da741e58d3926ad4d5.png)
Solution 5 (tangent cheese)
After getting ![]() , let
, let ![]() . Get the slopes of the lines
. Get the slopes of the lines ![]() and
and ![]() , namely
, namely ![]() ,
, ![]() . Then, use tangent angle subtraction to get
. Then, use tangent angle subtraction to get ![]() . Then, apply tangent double angle to get
. Then, apply tangent double angle to get ![]() . Solving, we obtain
. Solving, we obtain ![]() . Then, note that
. Then, note that ![]() , so
, so ![]() . Finishing off, we obtain
. Finishing off, we obtain ![]() .
.
~SigmaPiE
Video Solution
For those who want a video solution: (Is similar to Solution 1) https://youtu.be/WI2NVuIp1Ik
Video Solution by TheBeautyofMath
~IceMatrix
Video Solution by The Power of Logic
https://www.youtube.com/watch?v=sQIWSrio_Hc
~The Power of Logic
See Also
| 2019 AMC 10B (Problems • Answer Key • Resources) | ||
| Preceded by Problem 22 |
Followed by Problem 24 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
| 2019 AMC 12B (Problems • Answer Key • Resources) | |
| Preceded by Problem 19 |
Followed by Problem 21 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
These problems are copyrighted © by the Mathematical Association of America, as part of the American Mathematics Competitions. ![]()