2020 AIME II Problems/Problem 13
Contents
Problem
Convex pentagon ![]() has side lengths
has side lengths ![]() ,
, ![]() , and
, and ![]() . Moreover, the pentagon has an inscribed circle (a circle tangent to each side of the pentagon). Find the area of
. Moreover, the pentagon has an inscribed circle (a circle tangent to each side of the pentagon). Find the area of ![]() .
.
Solution 1
Assume the incircle touches ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() at
at ![]() respectively. Then let
respectively. Then let ![]() ,
, ![]() ,
, ![]() . So we have
. So we have ![]() ,
, ![]() and
and ![]() =7, solve it we have
=7, solve it we have ![]() ,
, ![]() ,
, ![]() . Let the center of the incircle be
. Let the center of the incircle be ![]() , by SAS we can proof triangle
, by SAS we can proof triangle ![]() is congruent to triangle
is congruent to triangle ![]() , and triangle
, and triangle ![]() is congruent to triangle
is congruent to triangle ![]() . Then we have
. Then we have ![]() ,
, ![]() . Extend
. Extend ![]() , cross ray
, cross ray ![]() at
at ![]() , ray
, ray ![]() at
at ![]() , then by AAS we have triangle
, then by AAS we have triangle ![]() is congruent to triangle
is congruent to triangle ![]() . Thus
. Thus ![]() . Let
. Let ![]() , then
, then ![]() . So by law of cosine in triangle
. So by law of cosine in triangle ![]() and triangle
and triangle ![]() we can obtain
we can obtain ![]() , solved it gives us
, solved it gives us ![]() , which yield triangle
, which yield triangle ![]() to be a triangle with side length 15, 15, 24, draw a height from
to be a triangle with side length 15, 15, 24, draw a height from ![]() to
to ![]() divides it into two triangles with side lengths 9, 12, 15, so the area of triangle
divides it into two triangles with side lengths 9, 12, 15, so the area of triangle ![]() is 108. Triangle
is 108. Triangle ![]() is a triangle with side lengths 6, 8, 10, so the area of two of them is 48, so the area of pentagon is
is a triangle with side lengths 6, 8, 10, so the area of two of them is 48, so the area of pentagon is ![]() .
.
-Fanyuchen20020715
Solution 2 (Complex Bash)
Suppose that the circle intersects ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() at
at ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() respectively. Then
respectively. Then ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . So
. So ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . Then
. Then ![]() , so
, so ![]() . Then we can solve for each individually.
. Then we can solve for each individually. ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . To find the radius, we notice that
. To find the radius, we notice that ![]() , or
, or ![]() . Each of these angles in this could be represented by complex numbers. When two complex numbers are multiplied, their angles add up to create the angle of the resulting complex number. Thus,
. Each of these angles in this could be represented by complex numbers. When two complex numbers are multiplied, their angles add up to create the angle of the resulting complex number. Thus, ![]() is real. Expanding, we get:
is real. Expanding, we get:
![]() , then
, then
![]() .
On the last expanding, we only multiply the reals with the imaginaries and vice versa, because we only care that the imaginary component equals 0.
.
On the last expanding, we only multiply the reals with the imaginaries and vice versa, because we only care that the imaginary component equals 0.
![]() .
.
![]()
![]() .
.
![]() must equal 4, as r cannot be negative or be approximately equal to 1.
Thus, the area of
must equal 4, as r cannot be negative or be approximately equal to 1.
Thus, the area of ![]() is
is ![]()
-nihao4112
Solution 3 (Guess)
This pentagon is very close to a regular pentagon with side lengths ![]() . The area of a regular pentagon with side lengths
. The area of a regular pentagon with side lengths ![]() is
is ![]() .
. ![]() is slightly greater than
is slightly greater than ![]() given that
given that ![]() is slightly less than
is slightly less than ![]() .
. ![]() is then slightly greater than
is then slightly greater than ![]() . We will approximate that to be
. We will approximate that to be ![]() . The area is now roughly
. The area is now roughly ![]() , but because the actual pentagon is not regular, but has the same perimeter of the regular one that we are comparing to we can say that this is an overestimate on the area and turn the
, but because the actual pentagon is not regular, but has the same perimeter of the regular one that we are comparing to we can say that this is an overestimate on the area and turn the ![]() into
into ![]() thus turning the area into
thus turning the area into ![]() which is
which is ![]() and since
and since ![]() is a multiple of the semiperimeter
is a multiple of the semiperimeter ![]() , we can safely say that the answer is most likely
, we can safely say that the answer is most likely ![]() .
.
~Lopkiloinm
Solution 4 (Guess)
Because the AIME answers have to be a whole number it would meant the radius of the circle have to be a whole number, thus by drawing the diagram and experimenting, we can safely say the radius is 4 and the answer is 60
(Edit: While the guess would be technically correct, the assumption that the radius would have to be a whole number for the ans to be a whole number is wrong)
By EtherealMidnight
Solution 5 (Official MAA 1)
Let ![]() be the inscribed circle,
be the inscribed circle, ![]() be its center, and
be its center, and ![]() be its radius. The area of
be its radius. The area of ![]() is equal to its semiperimeter,
is equal to its semiperimeter, ![]() times
times ![]() , so the problem is reduced to finding
, so the problem is reduced to finding ![]() . Let
. Let ![]() be the length of the tangent segment from
be the length of the tangent segment from ![]() to
to ![]() , and analogously define
, and analogously define ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . Then
. Then ![]() ,
, ![]() , and
, and ![]() , with a total of
, with a total of ![]() . Hence
. Hence ![]() ,
, ![]() , and
, and ![]() . It follows that
. It follows that ![]() and
and ![]() . Let
. Let ![]() be the point where
be the point where ![]() is tangent to
is tangent to ![]() . Then
. Then ![]() . The sum of the internal angles in polygons
. The sum of the internal angles in polygons ![]() and
and ![]() are equal, so
are equal, so ![]() , which implies that
, which implies that ![]() must be
must be ![]() . Therefore points
. Therefore points ![]() ,
, ![]() , and
, and ![]() are collinear.
are collinear.
![[asy] defaultpen(fontsize(8pt)); unitsize(0.025cm); pair[] vertices = {(0,0), (5,0), (8.6,4.8), (3.8,8.4), (-1.96, 6.72)}; string[] labels = {"$A$", "$B$", "$C$", "$D$", "$E$"}; pair[] dirs = {SW, SE,E, N, NW}; string[] smallLabels = {"$a$", "$b$", "$c$", "$d$", "$e$"}; pair I = (3,4); real rad = 4; pair Q = foot(I, vertices[2], vertices[3]); pair[] interpoints = {}; for(int i =0; i<vertices.length; ++i){ interpoints.push(foot(I, vertices[i], vertices[(i+1)%vertices.length])); } for(int i = 0; i< vertices.length; ++i){ draw(vertices[i]--vertices[(i+1)%vertices.length]); dot(labels[i],vertices[i],dirs[i]); draw(I--vertices[i]); } draw(Circle(I, rad)); dot("$I$", I, dir(200)); draw(I--Q); dot("$Q$", Q, NE); for(int i = 0; i < vertices.length; ++i){ label(smallLabels[i], vertices[i] --interpoints[i]); //dot(interpoints[i], blue); label(smallLabels[i], interpoints[(i-1)%vertices.length] -- vertices[i]); } [/asy]](http://latex.artofproblemsolving.com/0/4/9/049059ae12c804f8c02f35d5ccc0c92683085c54.png) Because
Because ![]() , it follows that
, it follows that![]() Another expression for
Another expression for ![]() can be found as follows. Note that
can be found as follows. Note that ![]() and
and ![]() , so
, so
![]() and
and
![]() Applying the Law of Cosines to
Applying the Law of Cosines to ![]() and
and ![]() gives
gives
![]() and
and
![]() Hence
Hence
![]() yielding
yielding
![]() equivalently
equivalently
![]() Substituting
Substituting ![]() gives the quadratic equation
gives the quadratic equation ![]() , with solutions
, with solutions ![]() , and
, and ![]() . The solution
. The solution ![]() corresponds to a five-pointed star, which is not convex. Indeed, if
corresponds to a five-pointed star, which is not convex. Indeed, if ![]() , then
, then ![]() ,
, ![]() , and
, and ![]() are less than
are less than ![]() implying that
implying that ![]() ,
, ![]() , and
, and ![]() are acute, which cannot happen in a convex pentagon. Thus
are acute, which cannot happen in a convex pentagon. Thus ![]() and
and ![]() . The requested area is
. The requested area is ![]() .
.
Solution 6 (Official MAA 2)
Define ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() as in Solution 5. Then, as in Solution 5,
as in Solution 5. Then, as in Solution 5, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . Let
. Let ![]() ,
, ![]() , and
, and ![]() . It follows that
. It follows that ![]() , so
, so ![]() . Thus
. Thus
![]()
![]() ,
, ![]() , and
, and ![]() . By the Tangent Addition Formula,
. By the Tangent Addition Formula,
![]() and
and
![\[\tan(2\beta + 2\gamma) = \frac{\frac{12r}{8-r^2}}{1-\frac{36r^2}{(8-r^2)^2}} = \frac{12r(8-r^2)}{(8-r^2)^2-36r^2}.\]](http://latex.artofproblemsolving.com/4/e/f/4ef015648462c699b9612d9bf6515c2be8d22276.png) Therefore
Therefore
![]() which simplifies to
which simplifies to ![]() . Then the solution proceeds as in Solution 5.
. Then the solution proceeds as in Solution 5.
Solution 7 (Official MAA 3)
Define ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() as in Solution 5. Note that
as in Solution 5. Note that
![]() Hence
Hence
![]() Therefore
Therefore
![]() Simplifying this equation gives the same quadratic equation in
Simplifying this equation gives the same quadratic equation in ![]() as in Solution 5.
as in Solution 5.
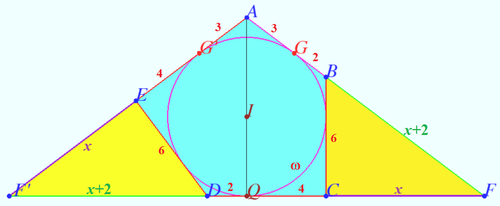
Solution 8 (The same circle)
Notation shown on diagram. As in solution 5, we get ![]() and so on.
and so on.
Let ![]() cross
cross ![]() at
at ![]() cross
cross ![]() at
at ![]()
![]()
![]()
Triangle ![]() has semiperimeter
has semiperimeter ![]()
The radius of incircle ![]() is
is
![]()
Triangle ![]() has semiperimeter
has semiperimeter ![]()
The radius of excircle ![]() is
is

It is the same radius, therefore
![]()
Then the solution proceeds as in Solution 5.
vladimir.shelomovskii@gmail.com, vvsss
Video Solution 1
https://youtu.be/bz5N-jI2e0U?t=327
Video Solution 2
| 2020 AIME II (Problems • Answer Key • Resources) | ||
| Preceded by Problem 12 |
Followed by Problem 14 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.