Difference between revisions of "2020 AMC 12A Problems/Problem 25"

Revision as of 02:11, 17 April 2021

Problem

The number $a=\frac{p}{q}$ , where $p$ and $q$ are relatively prime positive integers, has the property that the sum of all real numbers $x$ satisfying $\lfloor x \rfloor \cdot \{x\} = a \cdot x^2$ is $420$ , where $\lfloor x \rfloor$ denotes the greatest integer less than or equal to $x$ and $\{x\}=x- \lfloor x \rfloor$ denotes the fractional part of $x$ . What is $p+q$ ?

$\textbf{(A) } 245 \qquad \textbf{(B) } 593 \qquad \textbf{(C) } 929 \qquad \textbf{(D) } 1331 \qquad \textbf{(E) } 1332$

Solution 1

Let $1<k<2$ be the unique solution in this range. Note that $ck$ is also a solution as long as $ck < c+1$ , hence all our solutions are $k, 2k, ..., bk$ for some $b$ . This sum $420$ must be between $\frac{b(b+1)}{2}$ and $\frac{(b+1)(b+2)}{2}$ , which gives $b=28$ and $k=\frac{420}{406}=\frac{30}{29}$ . Plugging this back in gives $a=\frac{29 \cdot 1}{30^2} = \frac{29}{900} \implies \boxed{\textbf{C}}$ .

Solution 2

First note that $\lfloor x\rfloor \cdot \{x\}<0$ when $x<0$ while $ax^2\ge 0\forall x\in \mathbb{R}$ . Thus we only need to look at positive solutions ( $x=0$ doesn't affect the sum of the solutions). Next, we breakdown $\lfloor x\rfloor\cdot \{x\}$ down for each interval $[n,n+1)$ , where $n$ is a positive integer. Assume $\lfloor x\rfloor=n$ , then $\{x\}=x-n$ . This means that when $x\in [n,n+1)$ , $\lfloor x\rfloor \cdot \{x\}=n(x-n)=nx-n^2$ . Setting this equal to $ax^2$ gives $nx-n^2=ax^2\implies ax^2-nx+n^2=0 \implies x=\frac{n\pm \sqrt{n^2-4an^2}}{2a}$ We're looking at the solution with the positive $x$ , which is $x=\frac{n-n\sqrt{1-4a}}{2a}=\frac{n}{2a}\left(1-\sqrt{1-4a}\right)$ . Note that if $\lfloor x\rfloor=n$ is the greatest $n$ such that $\lfloor x\rfloor \cdot \{x\}=ax^2$ has a solution, the sum of all these solutions is slightly over $\sum_{k=1}^{n}k=\frac{n(n+1)}{2}$ , which is $406$ when $n=28$ , just under $420$ . Checking this gives $\sum_{k=1}^{28}\frac{k}{2a}\left(1-\sqrt{1-4a}\right)=\frac{1-\sqrt{1-4a}}{2a}\cdot 406=420$ $\frac{1-\sqrt{1-4a}}{2a}=\frac{420}{406}=\frac{30}{29}$ $29-29\sqrt{1-4a}=60a$ $29\sqrt{1-4a}=29-60a$ $29^2-4\cdot 29^2a=29^2+3600a^2-120\cdot 29a$ $3600a^2=116a$ $a=\frac{116}{3600}=\frac{29}{900} \implies \boxed{\textbf{(C) }929}$ ~ktong

Video Solution 1 (Geometry)

This video shows how things like The Pythagorean Theorem and The Law of Sines work together to solve this seemingly algebraic problem: https://www.youtube.com/watch?v=6IJ7Jxa98zw&feature=youtu.be

Video Solution 2

https://www.youtube.com/watch?v=xex8TBSzKNE ~ MathEx

Video Solution 3 (by Art of Problem Solving)

https://www.youtube.com/watch?v=7_mdreGBPvg&t=428s&ab_channel=ArtofProblemSolving

Created by Richard Rusczyk

Remarks of Solution 2 and Video Solution 3

Graph

Let $f(x)=\lfloor x \rfloor \cdot \{x\}.$

We make the following table of values:

$\begin{array}{c|c|c|clc} \boldsymbol{x} & \boldsymbol{\lfloor x \rfloor} & \boldsymbol{f(x)} & & \hspace{4mm}\textbf{Equation} & \\ [1.5ex] \hline & & & & & \\ [-1ex] [0,1) & 0 & 0 & & y=0 & \\ [1.5ex] [1,2) & 1 & [0,1) & & y=x-1 & \\ [1.5ex] [2,3) & 2 & [0,2) & & y=2x-4 & \\ [1.5ex] [3,4) & 3 & [0,3) & & y=3x-9 & \\ [1.5ex] [4,5) & 4 & [0,4) & & y=4x-16 & \\ [1.5ex] \cdots & \cdots & \cdots & & \ \ \ \ \ \ \ \cdots & \\ [1.5ex] [m,m+1) & m & [0,m) & & y=mx-m^2 & \end{array}$

We graph $f(x)$ by branches:

~MRENTHUSIASM (Graph by Desmos: https://www.desmos.com/calculator/ouvaiqjdzj)

Subtle Arguments

Visit the Discussion Page for the underlying arguments and additional questions.

~MRENTHUSIASM

@@ Line 35: / Line 35: @@
 ==Remarks of Solution 2 and Video Solution 3==
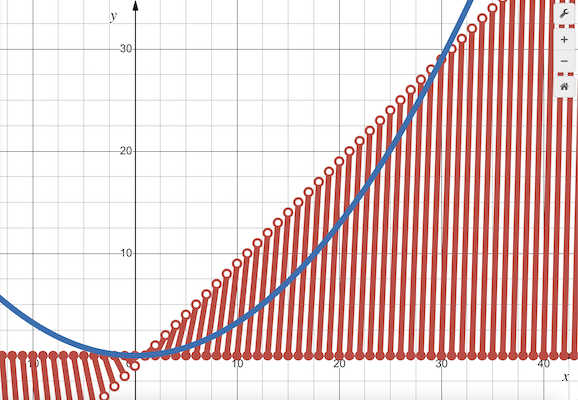
-Let <math>f(x)=\lfloor x \rfloor \cdot \{x\}</math> and <math>g(x)=a \cdot x^2.</math>
+===Graph===
+Let <math>f(x)=\lfloor x \rfloor \cdot \{x\}.</math>
-===Graph===
 We make the following table of values:
@@ Line 59: / Line 59: @@
 ~MRENTHUSIASM (Graph by Desmos: https://www.desmos.com/calculator/ouvaiqjdzj)
-===Claim===
+===Subtle Arguments===
-For all positive integers <math>n,</math> the first <math>n</math> <b>nonzero</b> solutions to <math>f(x)=g(x)</math> are of the form <cmath>x=m\left(\frac{1-\sqrt{1-4a}}{2a}\right),</cmath> where <math>m=1,2,3,\cdots,n.</math>
+Visit the [https://artofproblemsolving.com/wiki/index.php/Talk:2020_AMC_12A_Problems/Problem_25 Discussion Page] for the underlying arguments and additional questions.
-Equivalently, for <math>x>0,</math> the <math>n</math> intersections of the graphs of <math>f(x)</math> and <math>g(x)</math> occur in the consecutive branches of <math>f(x),</math> namely at <math>x\in[1,2),[2,3),[3,4),\cdots,[n,n+1).</math>
-~MRENTHUSIASM
-===Proof by Graph===
-Clearly, the equation <math>f(x)=g(x)</math> has no negative solutions, and its positive solutions all satisfy <math>x>1.</math> Moreover, none of its solutions is an integer.
-Note that the upper bounds of the branches of <math>f(x)</math> are along the line <math>h(x)=x-1</math> (excluded). <i><b>To prove the claim, we wish to show that for each branch of <math>\boldsymbol{f(x),}</math> there is exactly one solution for <math>\boldsymbol{f(x)=g(x)}</math> (from the branch <math>\boldsymbol{x\in[1,2)}</math> to the branch containing the larger solution of <math>\boldsymbol{g(x)=h(x)}</math>).</b></i> In 8:07-11:31 of [https://www.youtube.com/watch?v=7_mdreGBPvg&t=428s&ab_channel=ArtofProblemSolving Video Solution 3 (Art of Problem-Solving)], Mr. Rusczyk questions whether two solutions of <math>f(x)=g(x)</math> can be in the same branch of <math>f(x),</math> and he concludes that it is impossible in 16:25-16:43.
-We analyze the upper bound of <math>f(x):</math> Let <math>(c,c-1)</math> be one solution of <math>g(x)=h(x).</math> It is clear that <math>c>1.</math> We substitute this point to find <math>a:</math>
-<cmath>\begin{align*}
-g(c)&=h(c) \\
-ac^2&=c-1 \\
-a&=\frac{c-1}{c^2}.
-\end{align*}</cmath>
-We substitute this result back to find <math>x:</math>
-<cmath>\begin{align*}
-g(x)&=h(x) \\
-\left(\frac{c-1}{c^2}\right)x^2&=x-1 \\
-\left(\frac{c-1}{c^2}\right)x^2-x+1&=0 \\
-x^2-\left(\frac{c^2}{c-1}\right)x+\frac{c^2}{c-1}&=0 \ \ \ \ \ \ \ \ \ \ \ (*) \\
-(x-c)\left(x-\frac{c}{c-1}\right)&=0 \\
-x&=c,\ \frac{c}{c-1}.
-\end{align*}</cmath>
-By the way, using the precondition that <math>x=c</math> is a root of <math>(*),</math> we can factor its left side easily by the <b>Factor Theorem</b>. Note that <math>g(x)>h(x)</math> for all <math>x>\max{\left\{c, \frac{c}{c-1}\right\}},</math> as quadratic functions always outgrow linear functions.
-Now, we perform casework:
-<ol style="margin-left: 1.5em;">
-  <li><math>c=\frac{c}{c-1}>1\implies c=2</math> (Trivial Case)</li><p>
-It follows that the graphs of <math>g(x)</math> and <math>h(x)</math> only intersect at the point <math>(2,1),</math> which is not on the graph of <math>f(x).</math> So, the equation <math>f(x)=g(x)</math> has no solutions in this case, as the inequality <math>g(x)<h(x)</math> has no solutions.<p>
-  <li><math>c>\frac{c}{c-1}>1\implies c>2</math> and <math>1<\frac{c}{c-1}<2</math></li><p>
-It follows that for <math>g(x)=h(x),</math> the smaller solution is <math>x=\frac{c}{c-1}\in(1,2),</math> and <math>g(x)<h(x)</math> holds for all <math>x\in\left(\frac{c}{c-1},c\right).</math><p>
-By the <b>Intermediate Value Theorem</b>, for each branch of <math>f(x)</math> (where <math>x\in\left[\lfloor t\rfloor,\lfloor t\rfloor+1\right)</math>), we have <math>g(x)</math> in between its left output and its right "output", namely <cmath>0=f\left(\lfloor t\rfloor\right)<g\left(\lfloor x\rfloor\right)<h\left(\lfloor t\rfloor+1\right)=\lfloor t\rfloor.</cmath> Therefore, for the equation <math>f(x)=g(x),</math> there is exactly one solution for each branch of <math>f(x),</math> where <math>x\in\left(\frac{c}{c-1},c\right).</math> Now, the proof of the bolded sentence of paragraph 2 is complete.<p>
-  <li><math>\frac{c}{c-1}>c>1\implies 1<c<2</math> and <math>\frac{c}{c-1}>1</math></li><p>
-This case uses the same argument as Case 2. The smaller solution is <math>x=c\in(1,2),</math> and for each branch of <math>f(x),</math> where <math>x\in\left(c,\frac{c}{c-1}\right),</math> the equation <math>f(x)=g(x)</math> has exactly one solution.
-</ol>
 ~MRENTHUSIASM

2020 AMC 12A (Problems • Answer Key • Resources)
Preceded by Problem 24	Followed by Last Problem
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

Page

Toolbox

Search