Difference between revisions of "2020 AMC 12A Problems/Problem 25"
MRENTHUSIASM (talk | contribs) m (→Proof: Added in a space.) |
MRENTHUSIASM (talk | contribs) m |
||
| (42 intermediate revisions by the same user not shown) | |||
| Line 6: | Line 6: | ||
<math>\textbf{(A) } 245 \qquad \textbf{(B) } 593 \qquad \textbf{(C) } 929 \qquad \textbf{(D) } 1331 \qquad \textbf{(E) } 1332</math> | <math>\textbf{(A) } 245 \qquad \textbf{(B) } 593 \qquad \textbf{(C) } 929 \qquad \textbf{(D) } 1331 \qquad \textbf{(E) } 1332</math> | ||
| − | ==Solution 1== | + | ==Solution 1 (Comprehensive Solution in Algebra)== |
| + | Let <math>w=\lfloor x \rfloor</math> and <math>f=\{x\}</math> denote the whole part and the fractional part of <math>x,</math> respectively, for which <math>0\leq f<1</math> and <math>x=w+f.</math> | ||
| + | |||
| + | We rewrite the given equation as <cmath>w\cdot f=a\cdot(w+f)^2. \hspace{38.75mm}(1)</cmath> | ||
| + | Since <math>a\cdot(w+f)^2\geq0,</math> it follows that <math>w\cdot f\geq0,</math> from which <math>w\geq0.</math> | ||
| + | |||
| + | We expand and rearrange <math>(1)</math> as <cmath>af^2+(2a-1)wf+aw^2=0, \hspace{23mm}(2)</cmath> which is a quadratic with either <math>f</math> or <math>w.</math> | ||
| + | |||
| + | For simplicity purposes, we will treat <math>w</math> as some fixed nonnegative integer so that <math>(2)</math> is a quadratic with <math>f.</math> By the quadratic formula, we have | ||
| + | <cmath>\begin{align*} | ||
| + | f&=\frac{(1-2a)w\pm\sqrt{(2a-1)^2w^2-4a^2w^2}}{2a} \\ | ||
| + | &=w\Biggl(\frac{1-2a\pm\sqrt{(2a-1)^2-4a^2}}{2a}\Biggr) \\ | ||
| + | &=w\Biggl(\frac{1-2a\pm\sqrt{1-4a}}{2a}\Biggr). \hspace{25mm}(3) | ||
| + | \end{align*}</cmath> | ||
| + | |||
| + | If <math>w=0,</math> then <math>f=0.</math> We get <math>x=w+f=0,</math> which does not affect the sum of the solutions. Therefore, we consider the case for <math>w\geq1:</math> | ||
| + | |||
| + | Recall that <math>0\leq f<1,</math> so <math>\frac{1-2a\pm\sqrt{1-4a}}{2a}\geq0.</math> From the discriminant, we require that <math>1-4a\geq0,</math> or <math>a\leq\frac14.</math> Combining this with the precondition <math>a>0,</math> we need <cmath>0<a\leq\frac14. \hspace{54mm}(4)</cmath> | ||
| + | |||
| + | We consider each part of <math>0\leq f<1</math> separately: | ||
| + | <ol style="margin-left: 1.5em;"> | ||
| + | <li><math>f\geq0</math></li><p> | ||
| + | From <math>(2),</math> note that <math>a>0, (2a-1)w<0,</math> and <math>aw^2>0.</math> By Descartes' rule of signs, we deduce that <math>(2)</math> must have two positive roots, so <math>f\geq0</math> is always valid.<p> | ||
| + | Alternatively, from <math>(3)</math> and <math>(4),</math> note that all values of <math>a</math> for which <math>0<a\leq\frac14</math> satisfy <math>1-2a>\sqrt{1-4a}.</math> We deduce that both roots in <math>(3)</math> must be positive, so <math>f\geq0</math> is always valid.<p> | ||
| + | <li><math>f<1</math></li><p> | ||
| + | We rewrite <math>(3)</math> as <cmath>f=w\Biggl(\frac{1}{2a}-1\pm\frac{\sqrt{1-4a}}{2a}\Biggr).</cmath> From <math>(4),</math> it follows that <math>\frac{1}{2a}\geq\frac{1}{1/2}=2.</math> The larger root is | ||
| + | <cmath>\begin{align*} | ||
| + | f&\geq w\left(2-1+2\sqrt{1-4a}\right) \\ | ||
| + | &\geq 1\Biggl(2-1+2\sqrt{1-4\cdot\frac14}\Biggr) \\ | ||
| + | &= 1, \\ | ||
| + | \end{align*}</cmath> | ||
| + | which contradicts <math>f<1.</math> So, we take the smaller root, from which <cmath>f=w\Biggl(\frac{1}{2a}-1-\frac{\sqrt{1-4a}}{2a}\Biggr)</cmath> for some constant <math>k=\frac{1}{2a}-1-\frac{\sqrt{1-4a}}{2a}>0.</math> We rewrite <math>f</math> as <cmath>f=wk,</cmath> in which <math>f<1</math> is valid as long as <math>k<\frac 1w.</math> Note that the solutions of <math>x</math> are generated at <cmath>w=1,2,3,\cdots,W,</cmath> up to some value <math>w=W</math> such that <math>\frac{1}{W+1}\leq k<\frac1W.</math> | ||
| + | </ol> | ||
| + | Now, we express <math>x</math> in terms of <math>w</math> and <math>k:</math> | ||
| + | <cmath>\begin{align*} | ||
| + | x&=w+f \\ | ||
| + | &=w+wk \\ | ||
| + | &=w(1+k). | ||
| + | \end{align*}</cmath> | ||
| + | The sum of all solutions to the original equation is <cmath>\sum_{w=1}^{W}w(1+k)=(1+k)\cdot\sum_{w=1}^{W}w=(1+k)\cdot\frac{W(W+1)}{2}=420. \hspace{10mm}(\bigstar)</cmath> | ||
| + | As <math>1+k<1+\frac1W,</math> we conclude that <math>1+k</math> is slightly above <math>1</math> so that <math>\frac{W(W+1)}{2}</math> is slightly below <math>420,</math> or <math>W(W+1)</math> is slightly below <math>840.</math> By observations, we get <math>W=28.</math> Substituting this back into <math>(\bigstar)</math> produces <math>k=\frac{1}{29},</math> which satisfies <math>\frac{1}{W+1}\leq k<\frac1W,</math> as required. | ||
| + | |||
| + | Finally, we solve for <math>a</math> in <math>k=\frac{1}{2a}-1-\frac{\sqrt{1-4a}}{2a}:</math> | ||
| + | <cmath>\begin{align*} | ||
| + | \frac{1}{29}&=\frac{1}{2a}-1-\frac{\sqrt{1-4a}}{2a} \\ | ||
| + | \frac{2}{29}a&=1-2a-\sqrt{1-4a} \\ | ||
| + | \frac{60}{29}a-1&=-\sqrt{1-4a} \\ | ||
| + | \frac{60^2}{29^2}a^2-\frac{120}{29}a+1&=1-4a \\ | ||
| + | \frac{60^2}{29^2}a^2-\frac{4}{29}a&=0 \\ | ||
| + | a\left(\frac{60^2}{29^2}a-\frac{4}{29}\right)&=0. | ||
| + | \end{align*}</cmath> | ||
| + | Since <math>a>0,</math> we obtain <math>\frac{60^2}{29^2}a-\frac{4}{29}=0,</math> from which <cmath>a=\frac{4}{29}\cdot\frac{29^2}{60^2}=\frac{29}{900}.</cmath> | ||
| + | The answer is <math>29+900=\boxed{\textbf{(C) } 929}.</math> | ||
| + | |||
| + | ~MRENTHUSIASM (inspired by Math Jams's <b>2020 AMC 10/12A Discussion</b>) | ||
| + | |||
| + | ==Solution 2 (Condensed Version of Solution 1)== | ||
Let <math>1<k<2</math> be the unique solution in this range. Note that <math>ck</math> is also a solution as long as <math>ck < c+1</math>, hence all our solutions are <math>k, 2k, ..., bk</math> for some <math>b</math>. This sum <math>420</math> must be between <math>\frac{b(b+1)}{2}</math> and <math>\frac{(b+1)(b+2)}{2}</math>, which gives <math>b=28</math> and <math>k=\frac{420}{406}=\frac{30}{29}</math>. Plugging this back in gives <math>a=\frac{29 \cdot 1}{30^2} = \frac{29}{900} \implies \boxed{\textbf{C}}</math>. | Let <math>1<k<2</math> be the unique solution in this range. Note that <math>ck</math> is also a solution as long as <math>ck < c+1</math>, hence all our solutions are <math>k, 2k, ..., bk</math> for some <math>b</math>. This sum <math>420</math> must be between <math>\frac{b(b+1)}{2}</math> and <math>\frac{(b+1)(b+2)}{2}</math>, which gives <math>b=28</math> and <math>k=\frac{420}{406}=\frac{30}{29}</math>. Plugging this back in gives <math>a=\frac{29 \cdot 1}{30^2} = \frac{29}{900} \implies \boxed{\textbf{C}}</math>. | ||
| − | ==Solution | + | ==Solution 3== |
First note that <math>\lfloor x\rfloor \cdot \{x\}<0</math> when <math>x<0</math> while <math>ax^2\ge 0\forall x\in \mathbb{R}</math>. Thus we only need to look at positive solutions (<math>x=0</math> doesn't affect the sum of the solutions). | First note that <math>\lfloor x\rfloor \cdot \{x\}<0</math> when <math>x<0</math> while <math>ax^2\ge 0\forall x\in \mathbb{R}</math>. Thus we only need to look at positive solutions (<math>x=0</math> doesn't affect the sum of the solutions). | ||
Next, we breakdown <math>\lfloor x\rfloor\cdot \{x\}</math> down for each interval <math>[n,n+1)</math>, where <math>n</math> is a positive integer. Assume <math>\lfloor x\rfloor=n</math>, then <math>\{x\}=x-n</math>. This means that when <math>x\in [n,n+1)</math>, <math>\lfloor x\rfloor \cdot \{x\}=n(x-n)=nx-n^2</math>. Setting this equal to <math>ax^2</math> gives | Next, we breakdown <math>\lfloor x\rfloor\cdot \{x\}</math> down for each interval <math>[n,n+1)</math>, where <math>n</math> is a positive integer. Assume <math>\lfloor x\rfloor=n</math>, then <math>\{x\}=x-n</math>. This means that when <math>x\in [n,n+1)</math>, <math>\lfloor x\rfloor \cdot \{x\}=n(x-n)=nx-n^2</math>. Setting this equal to <math>ax^2</math> gives | ||
| Line 23: | Line 79: | ||
~ktong | ~ktong | ||
| − | == | + | ==Remark== |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Let <math>f(x)=\lfloor x \rfloor \cdot \{x\}</math> and <math>g(x)=a \cdot x^2.</math> | Let <math>f(x)=\lfloor x \rfloor \cdot \{x\}</math> and <math>g(x)=a \cdot x^2.</math> | ||
| − | |||
We make the following table of values: | We make the following table of values: | ||
<cmath>\begin{array}{c|c|c|clc} | <cmath>\begin{array}{c|c|c|clc} | ||
| − | \boldsymbol{x} & \boldsymbol{\lfloor x \rfloor} & \boldsymbol{f(x)} & & \textbf{ | + | & & & & & \\ [-1.5ex] |
| + | \boldsymbol{x} & \boldsymbol{\lfloor x \rfloor} & \boldsymbol{f(x)} & & \hspace{4mm}\textbf{Equation} & \\ [1.5ex] | ||
\hline | \hline | ||
& & & & & \\ [-1ex] | & & & & & \\ [-1ex] | ||
| Line 50: | Line 95: | ||
[4,5) & 4 & [0,4) & & y=4x-16 & \\ [1.5ex] | [4,5) & 4 & [0,4) & & y=4x-16 & \\ [1.5ex] | ||
\cdots & \cdots & \cdots & & \ \ \ \ \ \ \ \cdots & \\ [1.5ex] | \cdots & \cdots & \cdots & & \ \ \ \ \ \ \ \cdots & \\ [1.5ex] | ||
| − | [m,m+1) & m & [0,m) & & y=mx-m^2 & | + | [m,m+1) & m & [0,m) & & y=mx-m^2 & \\ [2ex] |
\end{array}</cmath> | \end{array}</cmath> | ||
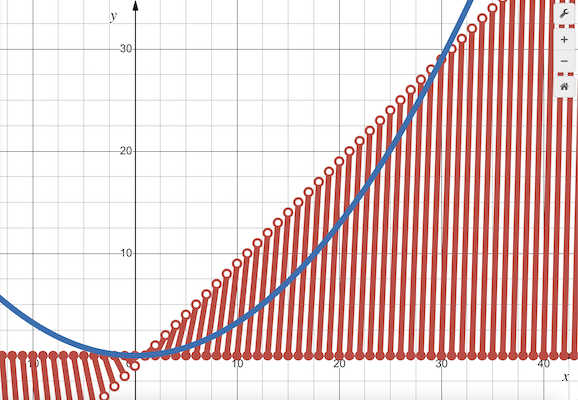
| − | We graph <math>f(x)</math> by branches | + | We graph <math>f(x)</math> (in red, by branches) and <math>g(x)</math> (in blue, for <math>a=\frac{29}{900}</math>) as shown below. |
[[File:2020 AMC 12A Problem 25.png|center]] | [[File:2020 AMC 12A Problem 25.png|center]] | ||
| − | + | Graph in Desmos: https://www.desmos.com/calculator/ouvaiqjdzj | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
~MRENTHUSIASM | ~MRENTHUSIASM | ||
| − | == | + | ==Video Solution 1 (Geometry)== |
| − | + | This video shows how things like The Pythagorean Theorem and The Law of Sines work together to solve this seemingly algebraic problem: https://www.youtube.com/watch?v=6IJ7Jxa98zw&feature=youtu.be | |
| − | + | ==Video Solution 2== | |
| + | https://www.youtube.com/watch?v=xex8TBSzKNE ~ MathEx | ||
| − | + | ==Video Solution 3 (by Art of Problem Solving)== | |
| − | + | https://www.youtube.com/watch?v=7_mdreGBPvg&t=428s&ab_channel=ArtofProblemSolving | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Created by Richard Rusczyk | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==See Also== | ==See Also== | ||
{{AMC12 box|year=2020|ab=A|num-b=24|after=Last Problem}} | {{AMC12 box|year=2020|ab=A|num-b=24|after=Last Problem}} | ||
{{MAA Notice}} | {{MAA Notice}} | ||
Revision as of 07:38, 14 June 2021
Contents
Problem
The number ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers, has the property that the sum of all real numbers
are relatively prime positive integers, has the property that the sum of all real numbers ![]() satisfying
satisfying
![]() is
is ![]() , where
, where ![]() denotes the greatest integer less than or equal to
denotes the greatest integer less than or equal to ![]() and
and ![]() denotes the fractional part of
denotes the fractional part of ![]() . What is
. What is ![]() ?
?
![]()
Solution 1 (Comprehensive Solution in Algebra)
Let ![]() and
and ![]() denote the whole part and the fractional part of
denote the whole part and the fractional part of ![]() respectively, for which
respectively, for which ![]() and
and ![]()
We rewrite the given equation as ![]() Since
Since ![]() it follows that
it follows that ![]() from which
from which ![]()
We expand and rearrange ![]() as
as ![]() which is a quadratic with either
which is a quadratic with either ![]() or
or ![]()
For simplicity purposes, we will treat ![]() as some fixed nonnegative integer so that
as some fixed nonnegative integer so that ![]() is a quadratic with
is a quadratic with ![]() By the quadratic formula, we have
By the quadratic formula, we have

If ![]() then
then ![]() We get
We get ![]() which does not affect the sum of the solutions. Therefore, we consider the case for
which does not affect the sum of the solutions. Therefore, we consider the case for ![]()
Recall that ![]() so
so ![]() From the discriminant, we require that
From the discriminant, we require that ![]() or
or ![]() Combining this with the precondition
Combining this with the precondition ![]() we need
we need ![]()
We consider each part of ![]() separately:
separately:
From ![]() note that
note that ![]() and
and ![]() By Descartes' rule of signs, we deduce that
By Descartes' rule of signs, we deduce that ![]() must have two positive roots, so
must have two positive roots, so ![]() is always valid.
is always valid.
Alternatively, from ![]() and
and ![]() note that all values of
note that all values of ![]() for which
for which ![]() satisfy
satisfy ![]() We deduce that both roots in
We deduce that both roots in ![]() must be positive, so
must be positive, so ![]() is always valid.
is always valid.
We rewrite ![]() as
as ![\[f=w\Biggl(\frac{1}{2a}-1\pm\frac{\sqrt{1-4a}}{2a}\Biggr).\]](http://latex.artofproblemsolving.com/f/b/f/fbf339570471c3d8838277de42d58142e07552f2.png) From
From ![]() it follows that
it follows that ![]() The larger root is
The larger root is
 which contradicts
which contradicts ![]() So, we take the smaller root, from which
So, we take the smaller root, from which ![\[f=w\Biggl(\frac{1}{2a}-1-\frac{\sqrt{1-4a}}{2a}\Biggr)\]](http://latex.artofproblemsolving.com/0/6/b/06b15412674320c8cc986e40e743c49bd3ff1119.png) for some constant
for some constant ![]() We rewrite
We rewrite ![]() as
as ![]() in which
in which ![]() is valid as long as
is valid as long as ![]() Note that the solutions of
Note that the solutions of ![]() are generated at
are generated at ![]() up to some value
up to some value ![]() such that
such that ![]()
Now, we express ![]() in terms of
in terms of ![]() and
and ![]()
 The sum of all solutions to the original equation is
The sum of all solutions to the original equation is ![\[\sum_{w=1}^{W}w(1+k)=(1+k)\cdot\sum_{w=1}^{W}w=(1+k)\cdot\frac{W(W+1)}{2}=420. \hspace{10mm}(\bigstar)\]](http://latex.artofproblemsolving.com/0/a/7/0a7c780d69fa818ae798ba64f8d082ee11c0b9a3.png) As
As ![]() we conclude that
we conclude that ![]() is slightly above
is slightly above ![]() so that
so that ![]() is slightly below
is slightly below ![]() or
or ![]() is slightly below
is slightly below ![]() By observations, we get
By observations, we get ![]() Substituting this back into
Substituting this back into ![]() produces
produces ![]() which satisfies
which satisfies ![]() as required.
as required.
Finally, we solve for ![]() in
in ![]()
 Since
Since ![]() we obtain
we obtain ![]() from which
from which ![]() The answer is
The answer is ![]()
~MRENTHUSIASM (inspired by Math Jams's 2020 AMC 10/12A Discussion)
Solution 2 (Condensed Version of Solution 1)
Let ![]() be the unique solution in this range. Note that
be the unique solution in this range. Note that ![]() is also a solution as long as
is also a solution as long as ![]() , hence all our solutions are
, hence all our solutions are ![]() for some
for some ![]() . This sum
. This sum ![]() must be between
must be between ![]() and
and ![]() , which gives
, which gives ![]() and
and ![]() . Plugging this back in gives
. Plugging this back in gives ![]() .
.
Solution 3
First note that ![]() when
when ![]() while
while ![]() . Thus we only need to look at positive solutions (
. Thus we only need to look at positive solutions (![]() doesn't affect the sum of the solutions).
Next, we breakdown
doesn't affect the sum of the solutions).
Next, we breakdown ![]() down for each interval
down for each interval ![]() , where
, where ![]() is a positive integer. Assume
is a positive integer. Assume ![]() , then
, then ![]() . This means that when
. This means that when ![]() ,
, ![]() . Setting this equal to
. Setting this equal to ![]() gives
gives
![]() We're looking at the solution with the positive
We're looking at the solution with the positive ![]() , which is
, which is ![]() . Note that if
. Note that if ![]() is the greatest
is the greatest ![]() such that
such that ![]() has a solution, the sum of all these solutions is slightly over
has a solution, the sum of all these solutions is slightly over ![]() , which is
, which is ![]() when
when ![]() , just under
, just under ![]() . Checking this gives
. Checking this gives
![\[\sum_{k=1}^{28}\frac{k}{2a}\left(1-\sqrt{1-4a}\right)=\frac{1-\sqrt{1-4a}}{2a}\cdot 406=420\]](http://latex.artofproblemsolving.com/b/5/1/b5129586fdf11baae2fb73ec8869a64d5fc09866.png)
![]()
![]()
![]()
![]()
![]()
![]() ~ktong
~ktong
Remark
Let ![]() and
and ![]()
We make the following table of values:
![\[\begin{array}{c|c|c|clc} & & & & & \\ [-1.5ex] \boldsymbol{x} & \boldsymbol{\lfloor x \rfloor} & \boldsymbol{f(x)} & & \hspace{4mm}\textbf{Equation} & \\ [1.5ex] \hline & & & & & \\ [-1ex] [0,1) & 0 & 0 & & y=0 & \\ [1.5ex] [1,2) & 1 & [0,1) & & y=x-1 & \\ [1.5ex] [2,3) & 2 & [0,2) & & y=2x-4 & \\ [1.5ex] [3,4) & 3 & [0,3) & & y=3x-9 & \\ [1.5ex] [4,5) & 4 & [0,4) & & y=4x-16 & \\ [1.5ex] \cdots & \cdots & \cdots & & \ \ \ \ \ \ \ \cdots & \\ [1.5ex] [m,m+1) & m & [0,m) & & y=mx-m^2 & \\ [2ex] \end{array}\]](http://latex.artofproblemsolving.com/5/1/3/513eba3b9a5aaf927bf101254e86ba7d0f2006c3.png)
We graph ![]() (in red, by branches) and
(in red, by branches) and ![]() (in blue, for
(in blue, for ![]() ) as shown below.
) as shown below.
Graph in Desmos: https://www.desmos.com/calculator/ouvaiqjdzj
~MRENTHUSIASM
Video Solution 1 (Geometry)
This video shows how things like The Pythagorean Theorem and The Law of Sines work together to solve this seemingly algebraic problem: https://www.youtube.com/watch?v=6IJ7Jxa98zw&feature=youtu.be
Video Solution 2
https://www.youtube.com/watch?v=xex8TBSzKNE ~ MathEx
Video Solution 3 (by Art of Problem Solving)
https://www.youtube.com/watch?v=7_mdreGBPvg&t=428s&ab_channel=ArtofProblemSolving
Created by Richard Rusczyk
See Also
| 2020 AMC 12A (Problems • Answer Key • Resources) | |
| Preceded by Problem 24 |
Followed by Last Problem |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.