Difference between revisions of "2020 AMC 12A Problems/Problem 25"
MRENTHUSIASM (talk | contribs) m (→Remark) |
(→Solution 1) |
||
| Line 6: | Line 6: | ||
<math>\textbf{(A) } 245 \qquad \textbf{(B) } 593 \qquad \textbf{(C) } 929 \qquad \textbf{(D) } 1331 \qquad \textbf{(E) } 1332</math> | <math>\textbf{(A) } 245 \qquad \textbf{(B) } 593 \qquad \textbf{(C) } 929 \qquad \textbf{(D) } 1331 \qquad \textbf{(E) } 1332</math> | ||
| − | ==Solution 1== | + | ==Solutions== |
| + | ===Solution 1=== | ||
| + | Let <math>x</math> be a root in the interval <math>(n,n+1)</math>. In this interval, <math>\lfloor x \rfloor = n</math> and <math>\{x\}=x-n</math>, so we must have <math>ax^2 = nx-n^2</math>, i.e. <cmath>x = \frac{n}{2a}\left(1 \pm \sqrt{1 -4a} \right) = \frac{2n}{1\mp \sqrt{1-4a}} </cmath>Notice that only one of the expressions gives a root in <math>(n,n+1)</math>: since <math>1- \sqrt{1-4a} < 1</math>, so <math>2n/(1- \sqrt{1-4a})>2n>n+1</math>. Thus <cmath>x = \frac{2n}{1+ \sqrt{1-4a}} =n\zeta.</cmath>Suppose <math>N</math> is the largest integer for which there is such a root; starting from <math>n<x<n+1</math> we get <cmath>\begin{align*} | ||
| + | n < x &= n\zeta < n+1 \\ | ||
| + | \Rightarrow \quad \tfrac 12 N(N+1) < 420 &= \tfrac 12 N(N+1)\zeta < \tfrac 12 N(N+3) | ||
| + | \end{align*}</cmath> From the right inequality we get <math>27< N</math> and from the left one we get <math>N<29</math>. Thus <math>N=28</math>. Using this in the middle equality we get <math>\zeta = \frac{30}{29}</math>, i.e. <cmath>a = \frac 14 \left[1-\left(\frac{2}{\zeta}-1\right)^2\right] = \frac 14 \left[1-\left(\frac{14}{15}\right)^2\right]= \frac{29}{900}.</cmath> | ||
| + | The answer is <math>29+900=\boxed{\textbf{(C) } 929}.</math> | ||
| + | |||
| + | ===Solution 2=== | ||
Let <math>w=\lfloor x \rfloor</math> and <math>f=\{x\}</math> denote the whole part and the fractional part of <math>x,</math> respectively, for which <math>0\leq f<1</math> and <math>x=w+f.</math> | Let <math>w=\lfloor x \rfloor</math> and <math>f=\{x\}</math> denote the whole part and the fractional part of <math>x,</math> respectively, for which <math>0\leq f<1</math> and <math>x=w+f.</math> | ||
Revision as of 20:35, 8 October 2021
Contents
Problem
The number ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers, has the property that the sum of all real numbers
are relatively prime positive integers, has the property that the sum of all real numbers ![]() satisfying
satisfying
![]() is
is ![]() , where
, where ![]() denotes the greatest integer less than or equal to
denotes the greatest integer less than or equal to ![]() and
and ![]() denotes the fractional part of
denotes the fractional part of ![]() . What is
. What is ![]() ?
?
![]()
Solutions
Solution 1
Let ![]() be a root in the interval
be a root in the interval ![]() . In this interval,
. In this interval, ![]() and
and ![]() , so we must have
, so we must have ![]() , i.e.
, i.e. ![]() Notice that only one of the expressions gives a root in
Notice that only one of the expressions gives a root in ![]() : since
: since ![]() , so
, so ![]() . Thus
. Thus ![]() Suppose
Suppose ![]() is the largest integer for which there is such a root; starting from
is the largest integer for which there is such a root; starting from ![]() we get
we get ![]() From the right inequality we get
From the right inequality we get ![]() and from the left one we get
and from the left one we get ![]() . Thus
. Thus ![]() . Using this in the middle equality we get
. Using this in the middle equality we get ![]() , i.e.
, i.e. ![\[a = \frac 14 \left[1-\left(\frac{2}{\zeta}-1\right)^2\right] = \frac 14 \left[1-\left(\frac{14}{15}\right)^2\right]= \frac{29}{900}.\]](http://latex.artofproblemsolving.com/2/0/6/2067eda80cf6801abaf542c04dc4bc6c769c9c37.png) The answer is
The answer is ![]()
Solution 2
Let ![]() and
and ![]() denote the whole part and the fractional part of
denote the whole part and the fractional part of ![]() respectively, for which
respectively, for which ![]() and
and ![]()
We rewrite the given equation as ![]() Since
Since ![]() it follows that
it follows that ![]() from which
from which ![]()
We expand and rearrange ![]() as
as ![]() which is a quadratic with either
which is a quadratic with either ![]() or
or ![]()
For simplicity purposes, we will treat ![]() as some fixed nonnegative integer so that
as some fixed nonnegative integer so that ![]() is a quadratic with
is a quadratic with ![]() By the Quadratic Formula, we have
By the Quadratic Formula, we have
 If
If ![]() then
then ![]() We get
We get ![]() which does not affect the sum of the solutions. Therefore, we consider the case for
which does not affect the sum of the solutions. Therefore, we consider the case for ![]()
Recall that ![]() so
so ![]() From the discriminant, we require that
From the discriminant, we require that ![]() or
or ![]() Combining this with the precondition
Combining this with the precondition ![]() we need
we need ![]()
We consider each part of ![]() separately:
separately:
From ![]() note that
note that ![]() and
and ![]() By Descartes' Rule of Signs, we deduce that
By Descartes' Rule of Signs, we deduce that ![]() must have two positive roots, so
must have two positive roots, so ![]() is always valid.
is always valid.
Alternatively, from ![]() and
and ![]() note that all values of
note that all values of ![]() for which
for which ![]() satisfy
satisfy ![]() We deduce that both roots in
We deduce that both roots in ![]() must be positive, so
must be positive, so ![]() is always valid.
is always valid.
We rewrite ![]() as
as ![\[f=w\Biggl(\frac{1}{2a}-1\pm\frac{\sqrt{1-4a}}{2a}\Biggr).\]](http://latex.artofproblemsolving.com/f/b/f/fbf339570471c3d8838277de42d58142e07552f2.png) From
From ![]() it follows that
it follows that ![]() The larger root is
The larger root is ![\[f\geq w\left(2-1+2\sqrt{1-4a}\right) \geq 1\Biggl(2-1+2\sqrt{1-4\cdot\frac14}\Biggr) = 1,\]](http://latex.artofproblemsolving.com/2/5/7/257f3a1d3ffe0009b0b4a96d8d69ee4b0ce9661b.png) which contradicts
which contradicts ![]() So, we take the smaller root, from which
So, we take the smaller root, from which ![\[f=w\Biggl(\frac{1}{2a}-1-\frac{\sqrt{1-4a}}{2a}\Biggr)\]](http://latex.artofproblemsolving.com/0/6/b/06b15412674320c8cc986e40e743c49bd3ff1119.png) for some constant
for some constant ![]() We rewrite
We rewrite ![]() as
as ![]() in which
in which ![]() is valid as long as
is valid as long as ![]() Note that the solutions of
Note that the solutions of ![]() are generated at
are generated at ![]() up to some value
up to some value ![]() such that
such that ![]()
Now, we express ![]() in terms of
in terms of ![]() and
and ![]()
![]() The sum of all solutions to the original equation is
The sum of all solutions to the original equation is ![\[\sum_{w=1}^{W}w(1+k)=(1+k)\cdot\sum_{w=1}^{W}w=(1+k)\cdot\frac{W(W+1)}{2}=420. \hspace{10mm}(\bigstar)\]](http://latex.artofproblemsolving.com/0/a/7/0a7c780d69fa818ae798ba64f8d082ee11c0b9a3.png) As
As ![]() we conclude that
we conclude that ![]() is slightly above
is slightly above ![]() so that
so that ![]() is slightly below
is slightly below ![]() or
or ![]() is slightly below
is slightly below ![]() By observations, we get
By observations, we get ![]() Substituting this into
Substituting this into ![]() produces
produces ![]() which satisfies
which satisfies ![]() as required.
as required.
Finally, we solve for ![]() in
in ![]()
 Since
Since ![]() we obtain
we obtain ![]() from which
from which ![]() The answer is
The answer is ![]()
~MRENTHUSIASM (inspired by Math Jams's 2020 AMC 10/12A Discussion)
Solution 2
First note that ![]() when
when ![]() while
while ![]() . Thus we only need to look at positive solutions (
. Thus we only need to look at positive solutions (![]() doesn't affect the sum of the solutions).
Next, we break
doesn't affect the sum of the solutions).
Next, we break ![]() down for each interval
down for each interval ![]() , where
, where ![]() is a positive integer. Assume
is a positive integer. Assume ![]() , then
, then ![]() . This means that when
. This means that when ![]() ,
, ![]() . Setting this equal to
. Setting this equal to ![]() gives
gives
![]() We're looking at the solution with the positive
We're looking at the solution with the positive ![]() , which is
, which is ![]() . Note that if
. Note that if ![]() is the greatest
is the greatest ![]() such that
such that ![]() has a solution, the sum of all these solutions is slightly over
has a solution, the sum of all these solutions is slightly over ![]() , which is
, which is ![]() when
when ![]() , just under
, just under ![]() . Checking this gives
. Checking this gives
 ~ktong
~ktong
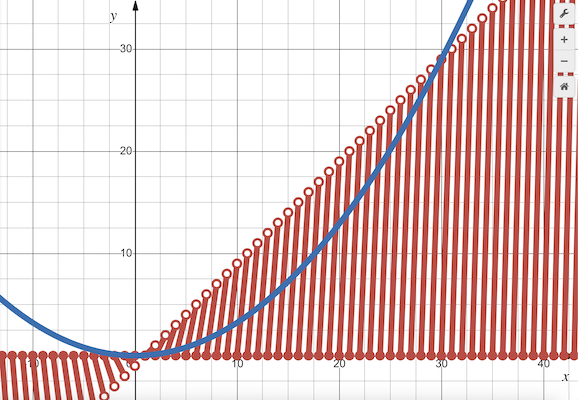
Remark
Let ![]() and
and ![]()
We make the following table of values:
![\[\begin{array}{c|c|c|l} & & & \\ [-2ex] \boldsymbol{x} & \boldsymbol{\lfloor x \rfloor} & \boldsymbol{f(x)} & \multicolumn{1}{c}{\textbf{Equation}} \\ [1.5ex] \hline & & & \\ [-1ex] [0,1) & 0 & 0 & y=0 \\ [1.5ex] [1,2) & 1 & [0,1) & y=x-1 \\ [1.5ex] [2,3) & 2 & [0,2) & y=2x-4 \\ [1.5ex] [3,4) & 3 & [0,3) & y=3x-9 \\ [1.5ex] [4,5) & 4 & [0,4) & y=4x-16 \\ [1.5ex] \cdots & \cdots & \cdots & \cdots \\ [1.5ex] [m,m+1) & m & [0,m) & y=mx-m^2 \\ [1.5ex] \end{array}\]](http://latex.artofproblemsolving.com/e/5/a/e5ae021b2075db17644b3b7694f376e63d2ccab1.png) We graph
We graph ![]() (in red, by branches) and
(in red, by branches) and ![]() (in blue, for
(in blue, for ![]() ) as shown below.
) as shown below.
Graph in Desmos: https://www.desmos.com/calculator/ouvaiqjdzj
~MRENTHUSIASM
Video Solution 1 (Geometry)
This video shows how things like The Pythagorean Theorem and The Law of Sines work together to solve this seemingly algebraic problem: https://www.youtube.com/watch?v=6IJ7Jxa98zw&feature=youtu.be
Video Solution 2
https://www.youtube.com/watch?v=xex8TBSzKNE ~ MathEx
Video Solution 3 (by Art of Problem Solving)
https://www.youtube.com/watch?v=7_mdreGBPvg&t=428s&ab_channel=ArtofProblemSolving
Created by Richard Rusczyk
See Also
| 2020 AMC 12A (Problems • Answer Key • Resources) | |
| Preceded by Problem 24 |
Followed by Last Problem |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.