Difference between revisions of "2020 AMC 12A Problems/Problem 25"
MRENTHUSIASM (talk | contribs) m (→Proof) |
MRENTHUSIASM (talk | contribs) m (→Proof) |
||
| Line 99: | Line 99: | ||
It follows that for <math>g(x)=h(x),</math> the smaller solution is <math>x=\frac{c}{c-1}\in(1,2),</math> and <math>g(x)<h(x)</math> holds for all <math>x\in\left(\frac{c}{c-1},c\right).</math> | It follows that for <math>g(x)=h(x),</math> the smaller solution is <math>x=\frac{c}{c-1}\in(1,2),</math> and <math>g(x)<h(x)</math> holds for all <math>x\in\left(\frac{c}{c-1},c\right).</math> | ||
| − | By the <b>Intermediate Value Theorem</b>, for each branch of <math>f(x)</math> (where <math>x\in\left[ | + | By the <b>Intermediate Value Theorem</b>, for each branch of <math>f(x)</math> (where <math>x\in\left[\lfloor t\rfloor,\lfloor t\rfloor+1\right)</math>), we have <math>g(x)</math> in between its left output and its right "output", namely <math>0=f\left(\lfloor t\rfloor\right)<g\left(\lfloor t\rfloor\right)<\lfloor t\rfloor.</math> Therefore, for the equation <math>f(x)=g(x),</math> there is exactly one solution for each branch of <math>f(x),</math> where <math>x\in\left(\frac{c}{c-1},c\right).</math> Now, the proof of the bolded sentence of paragraph 2 is complete. |
<math>\textbf{Case (3): }\boldsymbol{\frac{c}{c-1}>c>1\Longrightarrow 1<c<2} \textbf{ and } \boldsymbol{\frac{c}{c-1}>1}.</math> | <math>\textbf{Case (3): }\boldsymbol{\frac{c}{c-1}>c>1\Longrightarrow 1<c<2} \textbf{ and } \boldsymbol{\frac{c}{c-1}>1}.</math> | ||
Revision as of 11:05, 8 March 2021
Contents
Problem
The number ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers, has the property that the sum of all real numbers
are relatively prime positive integers, has the property that the sum of all real numbers ![]() satisfying
satisfying
![]() is
is ![]() , where
, where ![]() denotes the greatest integer less than or equal to
denotes the greatest integer less than or equal to ![]() and
and ![]() denotes the fractional part of
denotes the fractional part of ![]() . What is
. What is ![]() ?
?
![]()
Solution 1
Let ![]() be the unique solution in this range. Note that
be the unique solution in this range. Note that ![]() is also a solution as long as
is also a solution as long as ![]() , hence all our solutions are
, hence all our solutions are ![]() for some
for some ![]() . This sum
. This sum ![]() must be between
must be between ![]() and
and ![]() , which gives
, which gives ![]() and
and ![]() . Plugging this back in gives
. Plugging this back in gives ![]() .
.
Solution 2
First note that ![]() when
when ![]() while
while ![]() . Thus we only need to look at positive solutions (
. Thus we only need to look at positive solutions (![]() doesn't affect the sum of the solutions).
Next, we breakdown
doesn't affect the sum of the solutions).
Next, we breakdown ![]() down for each interval
down for each interval ![]() , where
, where ![]() is a positive integer. Assume
is a positive integer. Assume ![]() , then
, then ![]() . This means that when
. This means that when ![]() ,
, ![]() . Setting this equal to
. Setting this equal to ![]() gives
gives
![]() We're looking at the solution with the positive
We're looking at the solution with the positive ![]() , which is
, which is ![]() . Note that if
. Note that if ![]() is the greatest
is the greatest ![]() such that
such that ![]() has a solution, the sum of all these solutions is slightly over
has a solution, the sum of all these solutions is slightly over ![]() , which is
, which is ![]() when
when ![]() , just under
, just under ![]() . Checking this gives
. Checking this gives
![\[\sum_{k=1}^{28}\frac{k}{2a}\left(1-\sqrt{1-4a}\right)=\frac{1-\sqrt{1-4a}}{2a}\cdot 406=420\]](http://latex.artofproblemsolving.com/b/5/1/b5129586fdf11baae2fb73ec8869a64d5fc09866.png)
![]()
![]()
![]()
![]()
![]()
![]() ~ktong
~ktong
Video Solution 1 (Geometry)
This video shows how things like The Pythagorean Theorem and The Law of Sines work together to solve this seemingly algebraic problem: https://www.youtube.com/watch?v=6IJ7Jxa98zw&feature=youtu.be
Video Solution 2
https://www.youtube.com/watch?v=xex8TBSzKNE ~ MathEx
Video Solution 3 (by Art of Problem-Solving)
https://www.youtube.com/watch?v=7_mdreGBPvg&t=428s&ab_channel=ArtofProblemSolving
Created by Richard Rusczyk
Remarks of Solution 2 and Video Solution 3
Let ![]() and
and ![]()
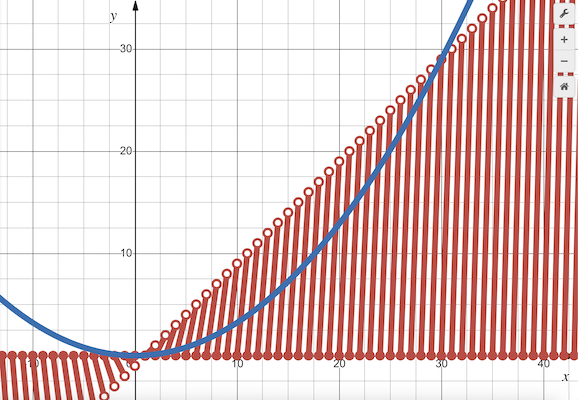
Graph
We make the following table of values:
![\[\begin{array}{c|c|c|clc} \boldsymbol{x} & \boldsymbol{\lfloor x \rfloor} & \boldsymbol{f(x)} & & \textbf{\ \ Equation} & \\ [1.5ex] \hline & & & & & \\ [-1ex] [0,1) & 0 & 0 & & y=0 & \\ [1.5ex] [1,2) & 1 & [0,1) & & y=x-1 & \\ [1.5ex] [2,3) & 2 & [0,2) & & y=2x-4 & \\ [1.5ex] [3,4) & 3 & [0,3) & & y=3x-9 & \\ [1.5ex] [4,5) & 4 & [0,4) & & y=4x-16 & \\ [1.5ex] \cdots & \cdots & \cdots & & \ \ \ \ \ \ \ \cdots & \\ [1.5ex] [m,m+1) & m & [0,m) & & y=mx-m^2 & \end{array}\]](http://latex.artofproblemsolving.com/2/8/2/282e782d8449ad251ef16c7cf087051678da3de4.png)
We graph ![]() by branches:
by branches:
~MRENTHUSIASM (Graph by Desmos: https://www.desmos.com/calculator/ouvaiqjdzj)
Claim
For all positive integers ![]() the first
the first ![]() nonzero solutions to
nonzero solutions to ![]() are of the form
are of the form ![]() where
where ![]()
Equivalently, for ![]() the
the ![]() intersections of the graphs of
intersections of the graphs of ![]() and
and ![]() occur in the consecutive branches of
occur in the consecutive branches of ![]() namely at
namely at ![]()
~MRENTHUSIASM
Proof
Clearly, the equation ![]() has no negative solutions, and its positive solutions all satisfy
has no negative solutions, and its positive solutions all satisfy ![]() Moreover, none of its solutions is an integer.
Moreover, none of its solutions is an integer.
Note that the upper bounds of the branches of ![]() are along the line
are along the line ![]() (excluded). To prove the claim, we wish to show that for each branch of
(excluded). To prove the claim, we wish to show that for each branch of ![]() there is exactly one solution for
there is exactly one solution for ![]() (from the branch
(from the branch ![]() to the branch containing the larger solution of
to the branch containing the larger solution of ![]() ). In 8:07-11:31 of Video Solution 3 (Art of Problem-Solving), Mr. Rusczyk questions whether two solutions of
). In 8:07-11:31 of Video Solution 3 (Art of Problem-Solving), Mr. Rusczyk questions whether two solutions of ![]() can be in the same branch of
can be in the same branch of ![]() and he concludes that it is impossible in 16:25-16:43.
and he concludes that it is impossible in 16:25-16:43.
We analyze the upper bound of ![]() Let
Let ![]() be one solution of
be one solution of ![]() It is clear that
It is clear that ![]() We substitute this point to find
We substitute this point to find ![]()

We substitute this result back to find ![]()
 By the way, using the precondition that
By the way, using the precondition that ![]() is a root of
is a root of ![]() we can factor its left side easily by the Factor Theorem. Note that
we can factor its left side easily by the Factor Theorem. Note that ![]() for all
for all ![]() as quadratic functions always outgrow linear functions.
as quadratic functions always outgrow linear functions.
Now, we perform casework:
![]()
It follows that the graphs of ![]() and
and ![]() only intersect at
only intersect at ![]() which is not on the graph of
which is not on the graph of ![]() So, the equation
So, the equation ![]() has no solution in this case, as the inequality
has no solution in this case, as the inequality ![]() has no solution.
has no solution.
![]()
It follows that for ![]() the smaller solution is
the smaller solution is ![]() and
and ![]() holds for all
holds for all ![]()
By the Intermediate Value Theorem, for each branch of ![]() (where
(where ![]() ), we have
), we have ![]() in between its left output and its right "output", namely
in between its left output and its right "output", namely ![]() Therefore, for the equation
Therefore, for the equation ![]() there is exactly one solution for each branch of
there is exactly one solution for each branch of ![]() where
where ![]() Now, the proof of the bolded sentence of paragraph 2 is complete.
Now, the proof of the bolded sentence of paragraph 2 is complete.
![]()
This case uses the same argument as ![]() The smaller solution is
The smaller solution is ![]() and for each branch of
and for each branch of ![]() where
where ![]() the equation
the equation ![]() has exactly one solution.
has exactly one solution.
~MRENTHUSIASM
See Also
| 2020 AMC 12A (Problems • Answer Key • Resources) | |
| Preceded by Problem 24 |
Followed by Last Problem |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.